（江蘇專版）2020年中考數(shù)學(xué)復(fù)習(xí) 第四單元 三角形 課時(shí)訓(xùn)練20 直角三角形與勾股定理

《（江蘇專版）2020年中考數(shù)學(xué)復(fù)習(xí) 第四單元 三角形 課時(shí)訓(xùn)練20 直角三角形與勾股定理》由會(huì)員分享，可在線閱讀，更多相關(guān)《（江蘇專版）2020年中考數(shù)學(xué)復(fù)習(xí) 第四單元 三角形 課時(shí)訓(xùn)練20 直角三角形與勾股定理（8頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

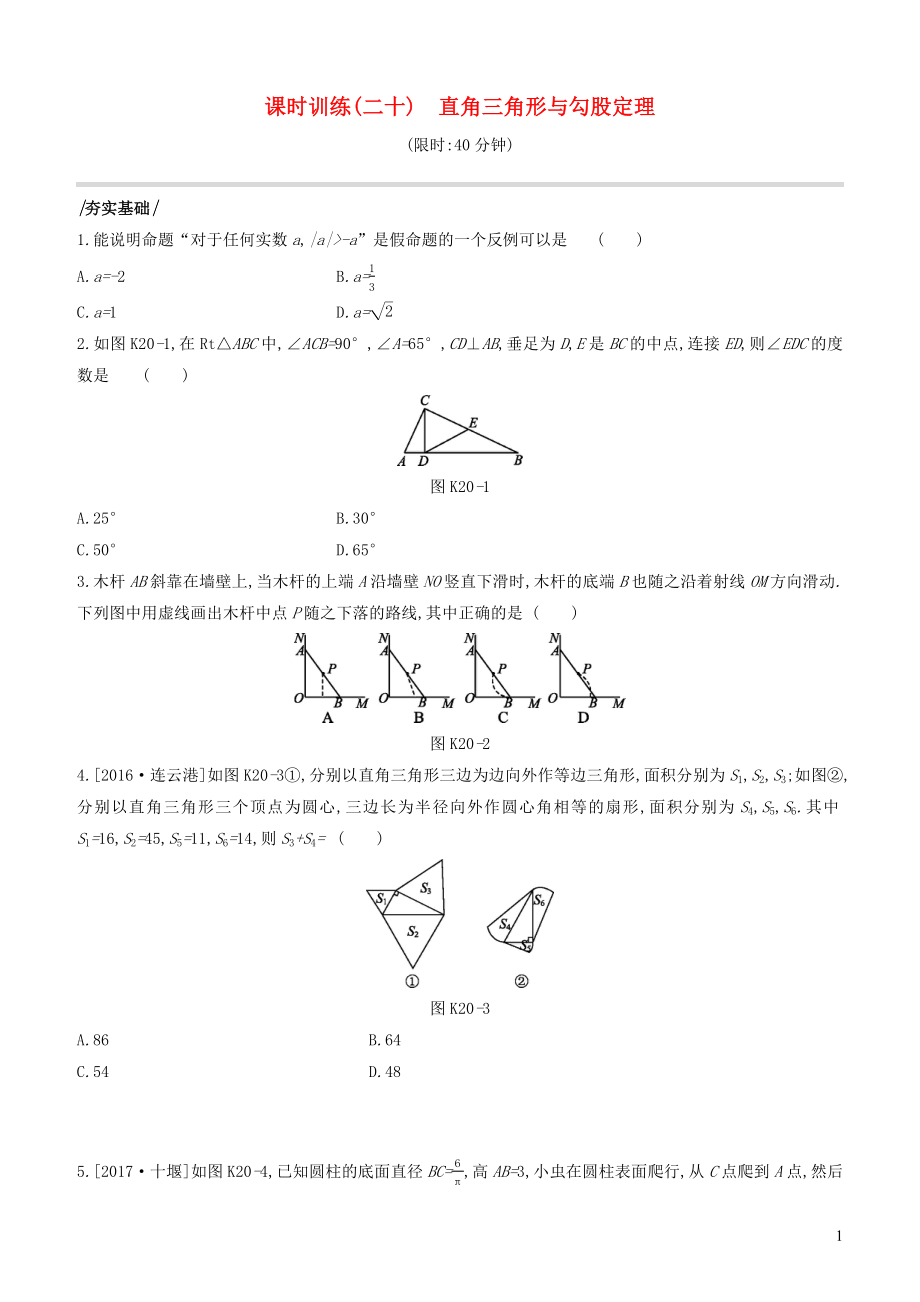
1、 課時(shí)訓(xùn)練(二十)　直角三角形與勾股定理 (限時(shí):40分鐘) |夯實(shí)基礎(chǔ)| 1.能說(shuō)明命題“對(duì)于任何實(shí)數(shù)a,|a|>-a”是假命題的一個(gè)反例可以是 ( ) A.a=-2 B.a=13 C.a=1 D.a=2 2.如圖K20-1,在Rt△ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂足為D,E是BC的中點(diǎn),連接ED,則∠EDC的度數(shù)是 (　　) 圖K20-1 A.25° B.30° C.50° D.65° 3.木桿AB斜靠在墻壁上,當(dāng)木桿的上端A沿墻壁NO豎直下滑時(shí),木桿的底端B也隨之沿著射

2、線OM方向滑動(dòng).下列圖中用虛線畫(huà)出木桿中點(diǎn)P隨之下落的路線,其中正確的是 ( ) 圖K20-2 4.[2016·連云港]如圖K20-3①,分別以直角三角形三邊為邊向外作等邊三角形,面積分別為S1,S2,S3;如圖②,分別以直角三角形三個(gè)頂點(diǎn)為圓心,三邊長(zhǎng)為半徑向外作圓心角相等的扇形,面積分別為S4,S5,S6.其中S1=16,S2=45,S5=11,S6=14,則S3+S4= ( ) 圖K20-3 A.86 B.64 C.54 D.48 5.[2017·十堰]如圖K20-4,已知圓柱的底面直徑BC=6π,高AB=3,小

3、蟲(chóng)在圓柱表面爬行,從C點(diǎn)爬到A點(diǎn),然后再沿另一面爬回C點(diǎn),則小蟲(chóng)爬行的最短路程為 (　　) 圖K20-4 A.32 B.35 C.65 D.62 6.數(shù)學(xué)文化[2019·大慶] 我國(guó)古代數(shù)學(xué)家趙爽的“勾股方圓圖”是由四個(gè)全等的直角三角形與中間的一個(gè)小正方形拼成的一個(gè)大正方形(如圖K20-5所示).如果大正方形的面積是13,小正方形的面積是1,直角三角形的兩直角邊長(zhǎng)分別為a,b,那么(a-b)2的值是　　　　.? 圖K20-5 7.[2019·宜賓] 如圖K20-6,已知直角三角形ABC中,CD是斜邊AB上的高,AC=4,BC=3,則AD=　　　　.? 圖K2

4、0-6 8.[2019·安順] 如圖K20-7,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,點(diǎn)D為斜邊BC上的一個(gè)動(dòng)點(diǎn),過(guò)D分別作DM⊥AB于點(diǎn)M,作DN⊥AC于點(diǎn)N,連接MN,則線段MN的最小值為　　　　.? 圖K20-7 9.數(shù)學(xué)文化[2017·麗水]我國(guó)三國(guó)時(shí)期數(shù)學(xué)家趙爽為了證明勾股定理,繪制了一幅“弦圖”,后人稱其為“趙爽弦圖”,如圖K20-8①所示.在圖②中,若正方形ABCD的邊長(zhǎng)為14,正方形IJKL的邊長(zhǎng)為2,且IJ∥AB,則正方形EFGH的邊長(zhǎng)為　　　　.? 圖K20-8 10.如圖K20-9,折疊矩形紙片ABCD,得折痕BD,再折疊使AD邊與對(duì)角

5、線BD重合,得折痕DF.若AB=4,BC=2,則AF=　　　　.? 圖K20-9 11.如圖K20-10,在△ABC中,∠ACB=120°,BC=4,D為AB的中點(diǎn),DC⊥BC,則△ABC的面積是　　　　.? 圖K20-10 12.[2019·鄂州] 如圖K20-11,已知線段AB=4,O是AB的中點(diǎn),直線l經(jīng)過(guò)點(diǎn)O,∠1=60°,P點(diǎn)是直線l上一點(diǎn),當(dāng)△APB為直角三角形時(shí),BP=　　　　.? 圖K20-11 13.[2019·巴中]如圖K20-12,等腰直角三角板如圖K20-12放置,直角頂點(diǎn)C在直線m上,分別過(guò)點(diǎn)A,B作AE⊥直線m于點(diǎn)E,BD⊥直線m于點(diǎn)D.

6、(1)求證:EC=BD; (2)若設(shè)△AEC三邊分別為a,b,c,利用此圖證明勾股定理. 圖K20-12 14.[2017·徐州]如圖K20-13,已知AC⊥BC,垂足為C,AC=4,BC=33,將線段AC繞點(diǎn)A按逆時(shí)針?lè)较蛐D(zhuǎn)60°,得到線段AD,連接DC,DB. (1)線段DC=　　　　;? (2)求線段DB的長(zhǎng)度. 圖K20-13 |拓展提升| 15.[2015·徐州]如圖K20-14,正方形ABCD的邊長(zhǎng)為1,以對(duì)角線AC為邊作第二個(gè)正方形ACEF,再以對(duì)角線AE為邊作第三個(gè)正方形AEGH,…,如此下去,第n個(gè)正方形的邊長(zhǎng)為　　　　.? 圖K20-

7、14 16.[2018·成都]如圖K20-15,在矩形ABCD中,按以下步驟作圖:①分別以點(diǎn)A和C為圓心,以大于12AC的長(zhǎng)為半徑作弧,兩弧相交于點(diǎn)M和N;②作直線MN交CD于點(diǎn)E,若DE=2,CE=3,則矩形的對(duì)角線AC的長(zhǎng)為　　　　.? 圖K20-15 17.[2018·重慶A卷]如圖K20-16,把三角形紙片折疊,使點(diǎn)B,點(diǎn)C都與點(diǎn)A重合,折痕分別為DE,FG,得到∠AGE=30°,若AE=EG=23厘米,則△ABC的邊BC的長(zhǎng)為　　　　厘米.? 圖K20-16 【參考答案】 1.A　[解析]說(shuō)明命題“對(duì)于任何實(shí)數(shù)a,|a|>-a”是假命題的一個(gè)反例可以是a=-2

8、,|-2|=2. 故選A. 2.D　[解析]因?yàn)镃D⊥AB,所以∠ADC=∠BDC=90°,所以∠ACD=90°-∠A=25°,因?yàn)椤螦CB=90°,所以∠DCE= 90°-∠ACD=65°,因?yàn)樵赗t△CDB中,E是BC的中點(diǎn),所以EC=ED,所以∠EDC=∠DCE=65°. 3.D　[解析]如圖,連接OP,由于OP是Rt△AOB斜邊上的中線,所以O(shè)P=12AB,不管木桿如何滑動(dòng),它的長(zhǎng)度不變,即OP是一個(gè)定值,點(diǎn)P就在以O(shè)為圓心,以O(shè)P長(zhǎng)為半徑的一段圓弧上,所以點(diǎn)P下落的路線是一段弧線.故選D. 4.C　[解析]如圖①,S1=34AC2,S2=34AB2,S3=34BC

9、2.∵AB2=AC2+BC2,∴S1+S3=34AC2+34BC2=34AB2=S2,∴S3=S2-S1. 如圖②,易求S4=S5+S6,∴S3+S4=S2-S1+S5+S6=45-16+11+14=54. 故選C. 5.D　[解析]把圓柱側(cè)面展開(kāi),展開(kāi)圖如圖所示,點(diǎn)A,C的最短距離為線段AC的長(zhǎng).在Rt△ABC中,∠ABC=90°,AB=3,∵CB為底面半圓弧長(zhǎng),∴CB=3,∴AC=32,∴從C點(diǎn)爬到A點(diǎn),然后再沿另一面爬回C點(diǎn),則小蟲(chóng)爬行的最短路程為2AC=62. 6.1　[解析](a-b)2=a2+b2-2ab,因?yàn)榇笳叫蔚拿娣e為13,所以由勾股定理可得,a2+b2=1

10、3,直角三角形面積=(13-1)÷4=3,即12ab=3,所以ab=6,所以(a-b)2=a2+b2-2ab=13-12=1. 7.165　[解析]在Rt△ABC中,AB=AC2+BC2=5,易證△ADC∽△ACB,∴ACAD=ABAC,∴AD=AC2AB=165,故答案為:165. 8.125　[解析]連接AD,∵DM⊥AB,DN⊥AC, ∴∠AMD=∠AND=90°, 又∵∠BAC=90°,∴四邊形AMDN是矩形, ∴MN=AD. ∵∠BAC=90°,AB=3,AC=4,∴BC=5, 當(dāng)AD⊥BC時(shí),AD最短, 此時(shí)△ABC的面積=12BC·AD=12AB·AC, ∴AD

11、的最小值=AB·ACBC=125, ∴線段MN的最小值為125. 9.10　[解析]設(shè)直角三角形的勾(較短的直角邊)為a,股(較長(zhǎng)的直角邊)為b,根據(jù)題意得a+b=14,b-a=2,解得a=6,b=8,由勾股定理得直角三角形的弦(斜邊)為62+82=100=10,即正方形EFGH的邊長(zhǎng)為10. 10.5-1　[解析]在Rt△ABD中,AB=4,AD=BC=2,∴BD=AB2+AD2=42+22=25,由折疊的性質(zhì)可得,△ADF≌△EDF,∴ED=AD=2,EF=AF,∴EB=BD-ED=25-2,設(shè)AF=x,則EF=AF=x,BF=4-x,在Rt△EBF中,x2+(25-2)2=(4-x

12、)2,解得x=5-1,即AF=5-1. 11.83　[解析]∵DC⊥BC,∴∠BCD=90°,∵∠ACB=120°,∴∠ACD=30°, 延長(zhǎng)CD到H使DH=CD,連接AH. ∵D為AB的中點(diǎn),∴AD=BD, 在△ADH與△BDC中,DH=CD,∠ADH=∠BDC,AD=BD, ∴△ADH≌△BDC(SAS), ∴AH=BC=4,∠H=∠BCD=90°, ∵∠ACH=30°, ∴CH=3AH=43, ∴CD=23, ∴△ABC的面積=2S△BCD=2×12×4×23=83,故答案為:83. 12.2或23或27　[解析]當(dāng)∠APB=90°時(shí),∵AO=OB=2,∠1=6

13、0°, ∴BP=OP=OB=2; 當(dāng)∠PAB=90°時(shí),∵∠AOP=60°, ∴AP=OA·tan∠AOP=23, ∴BP=AB2+AP2=27; 當(dāng)∠P'BA=90°時(shí),∵∠1=60°, ∴BP'=OB·tan∠1=23. 故答案為:2或23或27. 13.證明:(1)∵△ABC是等腰直角三角形,∠ACB=90°, ∴AC=BC,∠ACE+∠BCD=90°. ∵AE⊥EC,∴∠EAC+∠ACE=90°, ∴∠BCD=∠CAE. ∵BD⊥CD,∴∠AEC=∠CDB=90°, ∴△AEC≌△CDB(AAS),∴EC=BD. (2)∵△AEC≌△CDB, ∴BD=

14、EC=a,CD=AE=b,BC=AC=c, ∵S梯形AEDB=12(AE+BD)ED=12(a+b)(a+b),S梯形AEDB=12ab+12c2+12ab, ∴12(a+b)(a+b)=12ab+12c2+12ab, 整理可得a2+b2=c2,勾股定理得證. 14.解:(1)4 (2)∵AC=AD,∠CAD=60°, ∴△CAD是等邊三角形, ∴CD=AC=4,∠ACD=60°,過(guò)點(diǎn)D作DE⊥BC于E. ∵AC⊥BC,∠ACD=60°,∴∠BCD=30°. 在Rt△CDE中,CD=4,∠BCD=30°, ∴DE=12CD=2,CE=23,∴BE=3, 在Rt△DEB中,

15、由勾股定理得DB=7. 15.(2)n-1　[解析] ∵正方形ABCD的邊長(zhǎng)為1, ∴AC=AB2+BC2=2,∴第二個(gè)正方形的邊 長(zhǎng)為2,同理得第三個(gè)正方形的邊長(zhǎng)AE=2=(2)2,第四個(gè)正方形的邊長(zhǎng)AG=22=(2)3,…,因此第n個(gè)正方形的邊長(zhǎng)為(2)n-1,故答案為(2)n-1. 16.30　[解析]連接AE,由作圖可知MN為線段AC的垂直平分線,∴AE=CE=3,在Rt△ADE中,AE2=AD2+DE2,∴AD=AE2-DE2=5, 在Rt△ADC中,AC2=AD2+CD2, ∵CD=DE+CE=5, ∴AC=(5)2+52=30. 17.(43+6)　[解析]如圖,過(guò)點(diǎn)E作EM⊥AG于點(diǎn)M,則由AE=EG,得AG=2MG. ∵∠AGE=30°, EG=23厘米, ∴EM=12EG=3(厘米). 在Rt△EMG中,由勾股定理,得 MG=(23)2-(3)2=3(厘米),從而AG=6厘米. 由折疊可知,BE=AE=23厘米,GC=AG=6厘米. ∴BC=BE+EG+GC=23+23+6=43+6(厘米). 8