《【金版學案】2015-2016高中數(shù)學 3.2.2直線的兩點式方程練習 新人教A版必修2》由會員分享����,可在線閱讀�,更多相關(guān)《【金版學案】2015-2016高中數(shù)學 3.2.2直線的兩點式方程練習 新人教A版必修2(4頁珍藏版)》請在裝配圖網(wǎng)上搜索��。
1�����、
3.2.2 直線的兩點式方程
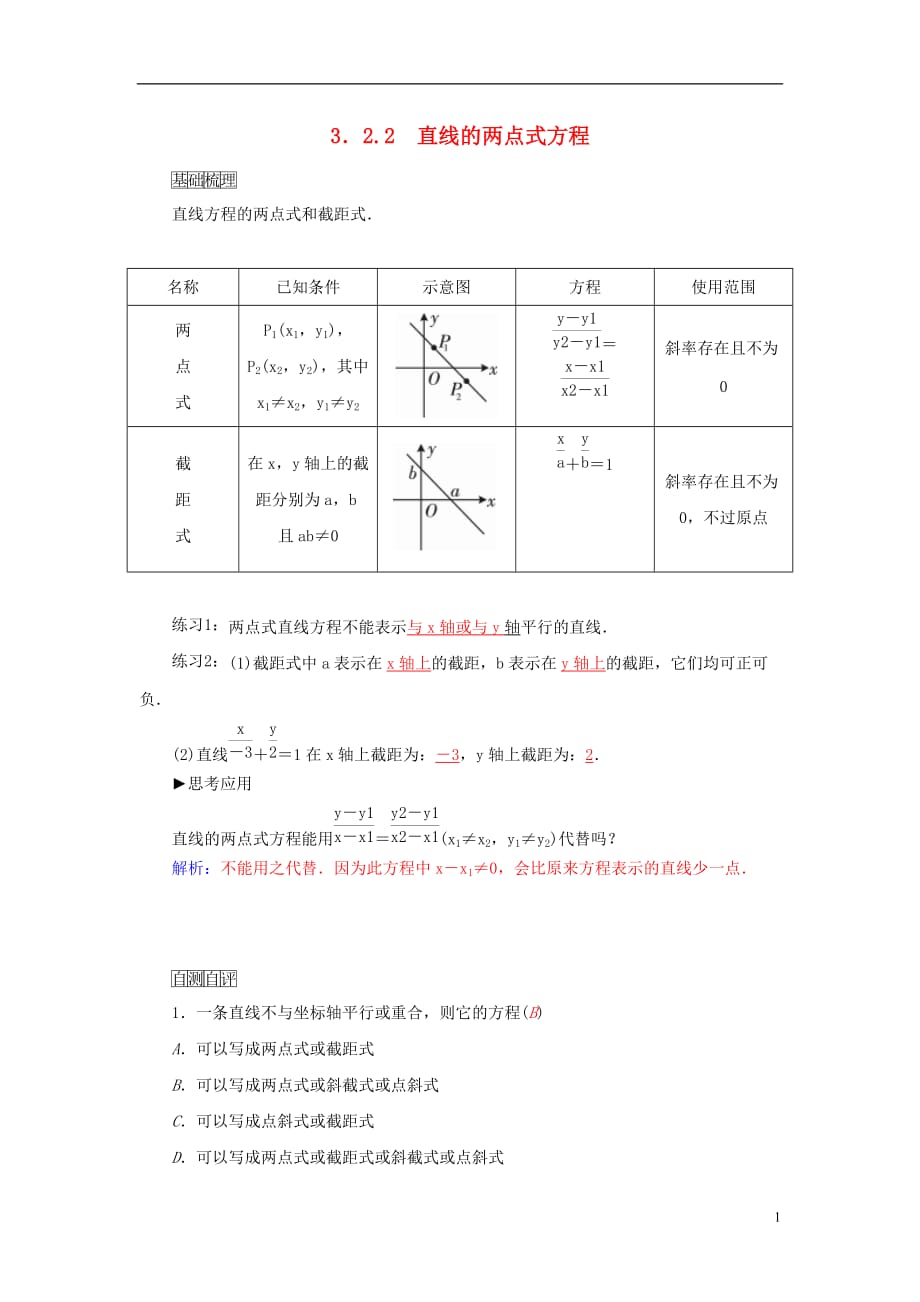
直線方程的兩點式和截距式.
名稱
已知條件
示意圖
方程
使用范圍
兩
點
式
P1(x1����,y1),P2(x2�����,y2)��,其中x1≠x2����,y1≠y2
=
斜率存在且不為0
截
距
式
在x,y軸上的截距分別為a���,b且ab≠0
+=1
斜率存在且不為0��,不過原點
兩點式直線方程不能表示與x軸或與y軸平行的直線.
(1)截距式中a表示在x軸上的截距���,b表示在y軸上的截距�,它們均可正可負.
(2)直線+=1在x軸上截距為:-3���,y軸上截距為:2.
?思考應(yīng)用
直線的兩點式方程能用=(x1≠x2��,y1
2��、≠y2)代替嗎?
解析:不能用之代替.因為此方程中x-x1≠0�����,會比原來方程表示的直線少一點.
1.一條直線不與坐標軸平行或重合��,則它的方程(B)
A.可以寫成兩點式或截距式
B.可以寫成兩點式或斜截式或點斜式
C.可以寫成點斜式或截距式
D.可以寫成兩點式或截距式或斜截式或點斜式
2.過兩點(6����,2),(3�,2)的直線方程是(B)
A.x=5 B.y=2
C.x+y=2 D.x=2
3.在x,y軸上的截距分別是-3����,4的直線方程是(A)
A.+=1 B.+=1
C.-=1 D.+=1
4.直線l過點(-1�����,0)和(2
3����、��,6)����,點(1 004,b)在直線l上�����,則b的值為(D)
A.2 007 B.2 008
C.2 009 D.2 010
解析:由兩點式可得直線方程為=��,
即y=2(x+1).點(1 004�,b)代入直線方程得,b=2(1 004+1)=2 010.
1.過P1(2�,0),P2(0�,3)兩點的直線方程是(B)
A.+=1 B.+=1
C.-=1 D.-=1
2.直線l:ax+y-2-a=0在x軸和y軸上的截距相等����,則a的值是(C)
A.1 B.-2
C.-2或1 D.2或1
解析:①令x=y(tǒng)=0得a=-2�,
②令x=0,得y=a+2���;令y=0�����,得x=.
4�����、
由a+2=得a=1.
3.下列四個命題中是真命題的是(B)
A.經(jīng)過定點P0(x0,y0)的直線都可以用方程y-y0=k(x-x0)表示
B.經(jīng)過任意兩個不同的點P1(x1�����,y1)�,P2(x2,y2)的直線都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示
C.不經(jīng)過原點的直線都可以用方程+=1表示
D.經(jīng)過定點A(0��,b)的直線都可以用方程y=kx+b表示
4.直線+=1過一�����、二、三象限�,則(C)
A.a(chǎn)>0,b>0 B.a(chǎn)>0����,b<0
C.a(chǎn)<0,b>0 D.a(chǎn)<0�����,b<0
解析:∵==1過一�����、二�、三象限,且a是x軸上的截距�����,b是y軸上的截距�����,
5、
∴a<0���,b>0.
5.若三角形ABC的頂點A(-5��,0)��,B(3���,-2),C(1�����,2)��,則經(jīng)過AB����、BC兩邊中點的直線方程為________.
答案:x-3y-2=0
6.過點C(-4�����,0)���,D(0����,-6)的直線的截距式方程是__________,化為斜截式方程是__________.
答案:+=1 y=-x-6
7.過點A(-1���,2)作直線l�,使它在x軸��、y軸上的截距相等�,則這樣的直線有(C)
A.4條 B.3條 C.2條 D.1條
解析:分截距為0和不為0的兩種情況討論,各有一條直線.
8.若三點A(2���,2)�����,B(a�,0)�����,C(0,b)(ab≠0)共線��,則+=
6����、________.
解析:設(shè)直線方程為+=1,
∴+=1��,∴+=.
答案:
9.已知直線l在x軸上的截距比在y軸上的截距大1��,且過定點(6�����,-2)�����,求直線l的方程.
解析:解法一 設(shè)直線l的點斜式方程為y+2=k(x-6)(k≠0).
令x=0�����,得y=-6k-2��;令y=0�����,得x=+6.
∴-(-6k-2)=1����,解得:k1=-或k2=-.
∴直線l的方程為y+2=-(x-6)或y+2=-(x-6).
即y=-x+2或y=-x+1.
解法二 設(shè)直線的斜截式方程為y=kx+b.
令y=0,則x=-.
依題意得:?或
∴直線l的方程為y=-x+1或y=-x+2.
解法三 設(shè)
7�����、直線l與y軸的交點為(0����,b),則直線方程的兩點式為=.
令y=0�,得x=.
∴=1+b,解得b1=1或b2=2.
∴直線l的方程為x+2y-2=0或2x+3y-6=0.
解法四 設(shè)直線方程的截距式為+=1����,又直線l過點(6,-2).∴+=1��,解得b1=1����,b2=2.
∴直線l的方程為+y=1或+=1.
即x+2y-2=0或2x+3y-6=0.
1.直線的兩點式方程既不能表示與x軸垂直的直線,也不能表示與y軸垂直的直線,但若把方程改寫成(x2-x1)(y-y1)-(y2-y1)(x-x1)=0則克服了這一缺點.
2.直線的截距式是兩點式的一個特殊情形����,用它來畫直線以及判斷直線經(jīng)過的象限或求直線與坐標軸圍成的三角形的面積比較方便,注意直線過原點或與坐標軸平行時�,沒有截距式方程,但直線過原點時兩截距存在且都等于0.
3.截距式既不能表示與坐標軸垂直的直線�,也不能表示過原點的直線.當遇直線在兩坐標上截距相等或是倍數(shù)關(guān)系時,務(wù)必考慮截距為0的情形.
4
 【金版學案】2015-2016高中數(shù)學 3.2.2直線的兩點式方程練習 新人教A版必修2
【金版學案】2015-2016高中數(shù)學 3.2.2直線的兩點式方程練習 新人教A版必修2