《2022年高中數(shù)學(xué) 第三章《回歸分析》教案2 新人教A版選修2-3》由會(huì)員分享�����,可在線閱讀����,更多相關(guān)《2022年高中數(shù)學(xué) 第三章《回歸分析》教案2 新人教A版選修2-3(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1、2022年高中數(shù)學(xué) 第三章《回歸分析》教案2 新人教A版選修2-3
一.問(wèn)題情境
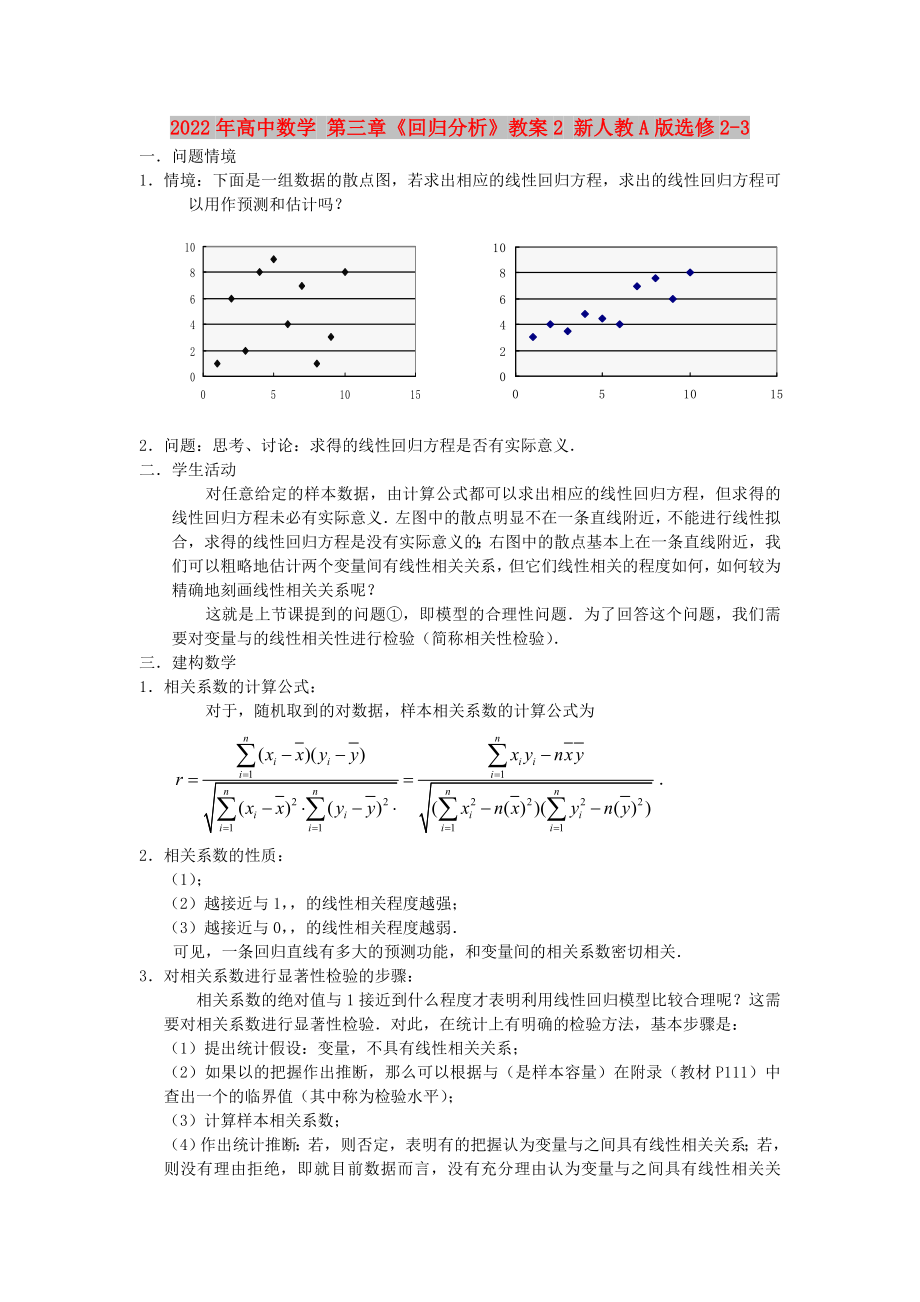
1.情境:下面是一組數(shù)據(jù)的散點(diǎn)圖����,若求出相應(yīng)的線性回歸方程,求出的線性回歸方程可以用作預(yù)測(cè)和估計(jì)嗎��?
2.問(wèn)題:思考�����、討論:求得的線性回歸方程是否有實(shí)際意義.
二.學(xué)生活動(dòng)
對(duì)任意給定的樣本數(shù)據(jù)�����,由計(jì)算公式都可以求出相應(yīng)的線性回歸方程�,但求得的線性回歸方程未必有實(shí)際意義.左圖中的散點(diǎn)明顯不在一條直線附近���,不能進(jìn)行線性擬合,求得的線性回歸方程是沒(méi)有實(shí)際意義的�����;右圖中的散點(diǎn)基本上在一條直線附近����,我們可以粗略地估計(jì)兩個(gè)變量間有線性相關(guān)關(guān)系,但它們線性相關(guān)的程度如何���,如何較為
2���、精確地刻畫線性相關(guān)關(guān)系呢?
這就是上節(jié)課提到的問(wèn)題①���,即模型的合理性問(wèn)題.為了回答這個(gè)問(wèn)題����,我們需要對(duì)變量與的線性相關(guān)性進(jìn)行檢驗(yàn)(簡(jiǎn)稱相關(guān)性檢驗(yàn)).
三.建構(gòu)數(shù)學(xué)
1.相關(guān)系數(shù)的計(jì)算公式:
對(duì)于��,隨機(jī)取到的對(duì)數(shù)據(jù),樣本相關(guān)系數(shù)的計(jì)算公式為
.
2.相關(guān)系數(shù)的性質(zhì):
(1)�����;
(2)越接近與1��,���,的線性相關(guān)程度越強(qiáng);
(3)越接近與0����,,的線性相關(guān)程度越弱.
可見(jiàn)�����,一條回歸直線有多大的預(yù)測(cè)功能����,和變量間的相關(guān)系數(shù)密切相關(guān).
3.對(duì)相關(guān)系數(shù)進(jìn)行顯著性檢驗(yàn)的步驟:
相關(guān)系數(shù)的絕對(duì)值與1接近到什么程度才表明利用線性回歸模型比較合理呢?這需要對(duì)相
3����、關(guān)系數(shù)進(jìn)行顯著性檢驗(yàn).對(duì)此,在統(tǒng)計(jì)上有明確的檢驗(yàn)方法,基本步驟是:
(1)提出統(tǒng)計(jì)假設(shè):變量���,不具有線性相關(guān)關(guān)系�����;
(2)如果以的把握作出推斷���,那么可以根據(jù)與(是樣本容量)在附錄(教材P111)中查出一個(gè)的臨界值(其中稱為檢驗(yàn)水平);
(3)計(jì)算樣本相關(guān)系數(shù)�����;
(4)作出統(tǒng)計(jì)推斷:若���,則否定����,表明有的把握認(rèn)為變量與之間具有線性相關(guān)關(guān)系�����;若���,則沒(méi)有理由拒絕�����,即就目前數(shù)據(jù)而言����,沒(méi)有充分理由認(rèn)為變量與之間具有線性相關(guān)關(guān)系.
說(shuō)明:1.對(duì)相關(guān)系數(shù)進(jìn)行顯著性檢驗(yàn),一般取檢驗(yàn)水平��,即可靠程度為.
2.這里的指的是線性相關(guān)系數(shù)��,的絕對(duì)值很小�,只是說(shuō)明線性相關(guān)程度低���,不一定不相關(guān)�����,可能是非線性相關(guān)
4�、的某種關(guān)系.
3.這里的是對(duì)抽樣數(shù)據(jù)而言的.有時(shí)即使��,兩者也不一定是線性相關(guān)的.故在統(tǒng)計(jì)分析時(shí)��,不能就數(shù)據(jù)論數(shù)據(jù),要結(jié)合實(shí)際情況進(jìn)行合理解釋.
4.對(duì)于上節(jié)課的例1,可按下面的過(guò)程進(jìn)行檢驗(yàn):
(1)作統(tǒng)計(jì)假設(shè):與不具有線性相關(guān)關(guān)系��;
(2)由檢驗(yàn)水平與在附錄中查得�;
(3)根據(jù)公式得相關(guān)系數(shù);
(4)因?yàn)?�,即���,所以有﹪的把握認(rèn)為與之間具有線性相關(guān)關(guān)系,線性回歸方程為是有意義的.
四.?dāng)?shù)學(xué)運(yùn)用
1.例題:
例1.下表是隨機(jī)抽取的對(duì)母女的身高數(shù)據(jù),試根據(jù)這些數(shù)據(jù)探討與之間的關(guān)系.
母親身高
女兒身高
解:所給數(shù)
5����、據(jù)的散點(diǎn)圖如圖所示:由圖可以看出���,這些點(diǎn)在一條直線附近����,
因?yàn)?���,?
,
�,
,
所以�����,
由檢驗(yàn)水平及,在附錄中查得�����,因?yàn)?所以可以認(rèn)為與之間具有較強(qiáng)的線性相關(guān)關(guān)系.線性回歸模型中的估計(jì)值分別為
��,
故對(duì)的線性回歸方程為.
例2.要分析學(xué)生高中入學(xué)的數(shù)學(xué)成績(jī)對(duì)高一年級(jí)數(shù)學(xué)學(xué)習(xí)的影響��,在高一年級(jí)學(xué)生中隨機(jī)抽取名學(xué)生����,分析他們?nèi)雽W(xué)的數(shù)學(xué)成績(jī)和高一年級(jí)期末數(shù)學(xué)考試成績(jī)?nèi)缦卤恚?
學(xué)生編號(hào)
入學(xué)成績(jī)
高一期末成績(jī)
(1)計(jì)算入學(xué)成績(jī)與高一期末成績(jī)的相關(guān)系數(shù);
(2)如果與之間具有線性相關(guān)關(guān)系��,求線性回歸方程��;
(3)若某學(xué)生入學(xué)數(shù)學(xué)成績(jī)?yōu)榉?���,試估?jì)他高一期末數(shù)學(xué)考試成績(jī).
解:(1)因?yàn)?����,?
,����,
.
因此求得相關(guān)系數(shù)為.
結(jié)果說(shuō)明這兩組數(shù)據(jù)的相關(guān)程度是比較高的;
小結(jié)解決這類問(wèn)題的解題步驟:
(1)作出散點(diǎn)圖��,直觀判斷散點(diǎn)是否在一條直線附近�;
(2)求相關(guān)系數(shù);
(3)由檢驗(yàn)水平和的值在附錄中查出臨界值���,判斷與是否具有較強(qiáng)的線性相關(guān)關(guān)系����;
(4)計(jì)算��,����,寫出線性回歸方程.
 2022年高中數(shù)學(xué) 第三章《回歸分析》教案2 新人教A版選修2-3
2022年高中數(shù)學(xué) 第三章《回歸分析》教案2 新人教A版選修2-3