2022九年級(jí)數(shù)學(xué)上冊(cè) 第4章 圖形的相似4.6 利用相似三角形測(cè)高學(xué)案（新版）北師大版

《2022九年級(jí)數(shù)學(xué)上冊(cè) 第4章 圖形的相似4.6 利用相似三角形測(cè)高學(xué)案（新版）北師大版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022九年級(jí)數(shù)學(xué)上冊(cè) 第4章 圖形的相似4.6 利用相似三角形測(cè)高學(xué)案（新版）北師大版（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

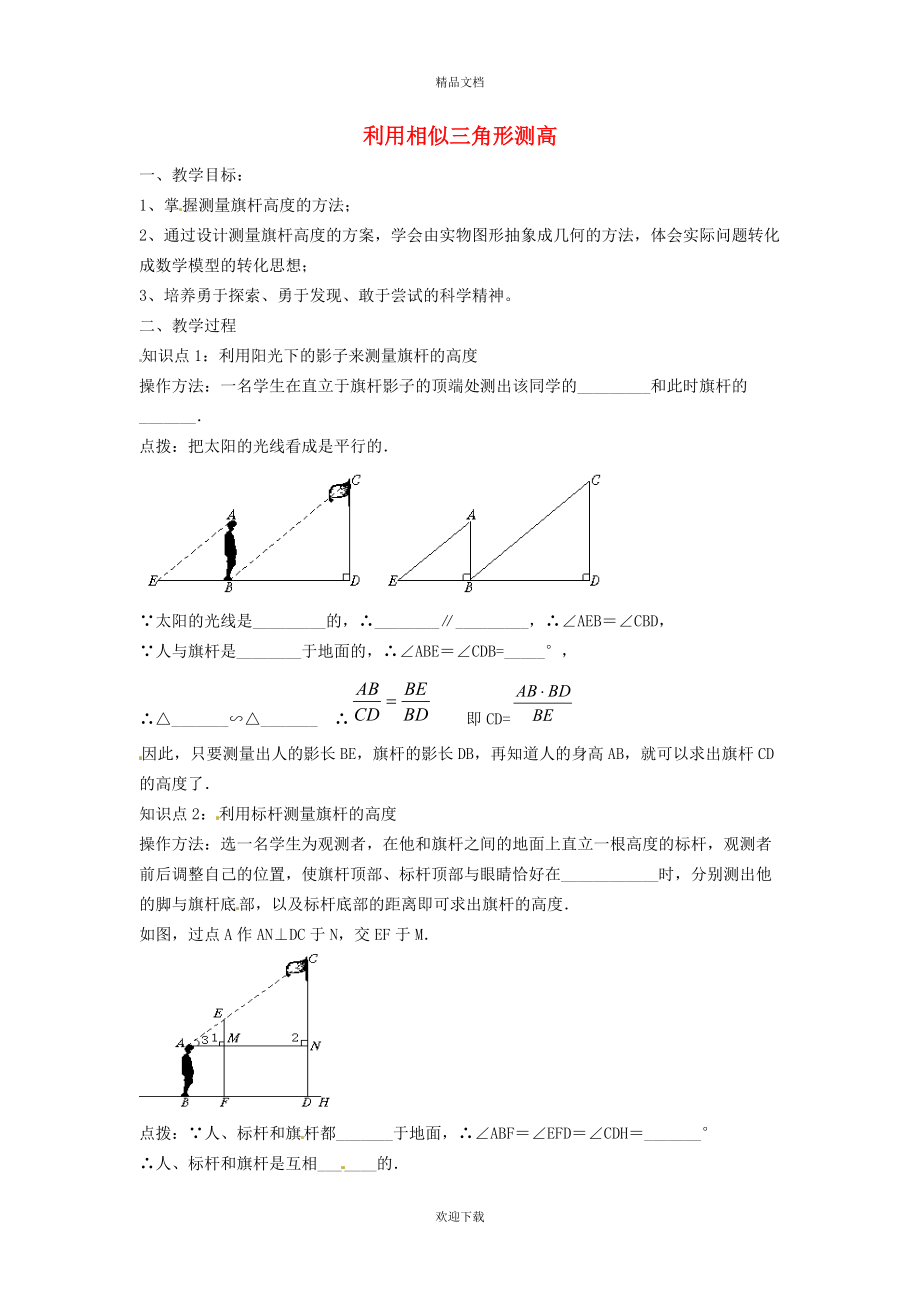
1、精品文檔 利用相似三角形測(cè)高 一、教學(xué)目標(biāo)： 1、掌握測(cè)量旗桿高度的方法； 2、通過(guò)設(shè)計(jì)測(cè)量旗桿高度的方案，學(xué)會(huì)由實(shí)物圖形抽象成幾何的方法，體會(huì)實(shí)際問(wèn)題轉(zhuǎn)化成數(shù)學(xué)模型的轉(zhuǎn)化思想； 3、培養(yǎng)勇于探索、勇于發(fā)現(xiàn)、敢于嘗試的科學(xué)精神。 二、教學(xué)過(guò)程 知識(shí)點(diǎn)1：利用陽(yáng)光下的影子來(lái)測(cè)量旗桿的高度 操作方法：一名學(xué)生在直立于旗桿影子的頂端處測(cè)出該同學(xué)的_________和此時(shí)旗桿的_______． 點(diǎn)撥：把太陽(yáng)的光線看成是平行的． ∵太陽(yáng)的光線是_________的，∴________∥_________，∴∠AEB＝∠CBD， ∵人與旗桿是________于地面的，∴∠ABE＝

2、∠CDB=_____°， ∴△_______∽△_______ ∴ 即CD= 因此，只要測(cè)量出人的影長(zhǎng)BE，旗桿的影長(zhǎng)DB，再知道人的身高AB，就可以求出旗桿CD的高度了． 知識(shí)點(diǎn)2：利用標(biāo)桿測(cè)量旗桿的高度 操作方法：選一名學(xué)生為觀測(cè)者，在他和旗桿之間的地面上直立一根高度的標(biāo)桿，觀測(cè)者前后調(diào)整自己的位置，使旗桿頂部、標(biāo)桿頂部與眼睛恰好在____________時(shí)，分別測(cè)出他的腳與旗桿底部，以及標(biāo)桿底部的距離即可求出旗桿的高度． 如圖，過(guò)點(diǎn)A作AN⊥DC于N，交EF于M． 點(diǎn)撥：∵人、標(biāo)桿和旗桿都_______于地面，∴∠ABF＝∠EFD＝∠CDH＝_______° ∴

3、人、標(biāo)桿和旗桿是互相_______的． ∵EF∥CN，∴∠_____＝∠_____，∵∠3＝∠3， ∴△______∽△______，∴ ∵人與標(biāo)桿的距離、人與旗桿的距離，標(biāo)桿與人的身高的差EM都已測(cè)量出， ∴能求出CN，∵∠ABF＝∠CDF＝∠AND＝90°，∴四邊形ABND為________． ∴DN＝_______，∴能求出旗桿CD的長(zhǎng)度． 知識(shí)點(diǎn)3：利用鏡子的反射 操作方法：選一名學(xué)生作為觀測(cè)者．在他與旗桿之間的地面上平放一面鏡子，固定鏡子的位置，觀測(cè)者看著鏡子來(lái)回調(diào)整自己的位置，使自己能夠通過(guò)鏡子看到旗桿_______．測(cè)出此時(shí)他的腳與鏡子的距離、旗桿底部與鏡子的距離就

4、能求出旗桿的高度． 點(diǎn)撥：入射角＝反射角 ∵入射角＝反射角 ∴∠________＝∠________ ∵人、旗桿都_________于地面 ∴∠B＝∠D＝_______° ∴△________∽△________，∴ 因此，測(cè)量出人與鏡子的距離BE，旗桿與鏡子的距離DE，再知道人的身高AB，就可以求出旗桿CD的高度． 活動(dòng)的考前須知： ①運(yùn)用方法1時(shí)可以把太陽(yáng)光近似地看成平行光線，計(jì)算時(shí)還要用到觀測(cè)者的身高． ②運(yùn)用方法2時(shí)觀測(cè)者的眼睛必須與標(biāo)桿的頂端和旗桿的頂端“三點(diǎn)共線〞，標(biāo)桿與地面要垂直，在計(jì)算時(shí)還要用到觀測(cè)者的眼睛離地面的高度． ③運(yùn)用方法3時(shí)應(yīng)注

5、意向?qū)W生解釋光線的入射角等于反射角的現(xiàn)象． 三、達(dá)標(biāo)測(cè)試： 1．小明的身高是1.6m，他的影長(zhǎng)是2m，同一時(shí)刻一古塔的影長(zhǎng)是18m，那么該古塔的高度是多少？ 2．高4m的旗桿在水平地面上的影子長(zhǎng)6m，此時(shí)測(cè)得附近一個(gè)建筑物的影子長(zhǎng)24m，求該建筑物的高度？ 3．旗桿的影子長(zhǎng)6m，同時(shí)測(cè)得旗桿頂端到其影子頂端的距離是10m，如果此時(shí)附近小樹的影子長(zhǎng)3m，那么小樹有多高？ A B C N M 4．如圖，AB表示一個(gè)窗戶的高，AM和BN表示射入室內(nèi)的光線，窗戶的下端到地面的距離BC=1m，某一時(shí)刻BC在地面的影長(zhǎng)CN=1.5m，AC在地面的影長(zhǎng)CM=4.5m，求窗戶的高度？ 5.如圖，王華晚上由路燈A下的B處走到C處時(shí)，測(cè)得影長(zhǎng)CD的長(zhǎng)為1米，繼續(xù)往前走3米到達(dá)E處時(shí)，測(cè)得影子EF的長(zhǎng)為2米，王華的身高是1.5米，那么路燈A的高度AB為多少米？ 歡迎下載