《安徽省中考數(shù)學(xué)總復(fù)習(xí) 第一輪 考點系統(tǒng)復(fù)習(xí) 第三單元 函數(shù) 第12講 二次函數(shù) 第1課時 二次函數(shù)的圖象和性質(zhì)試題》由會員分享,可在線閱讀����,更多相關(guān)《安徽省中考數(shù)學(xué)總復(fù)習(xí) 第一輪 考點系統(tǒng)復(fù)習(xí) 第三單元 函數(shù) 第12講 二次函數(shù) 第1課時 二次函數(shù)的圖象和性質(zhì)試題(4頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1���、▼▼▼2019屆數(shù)學(xué)中考復(fù)習(xí)資料▼▼▼
二次函數(shù)
第1課時 二次函數(shù)的圖象和性質(zhì)
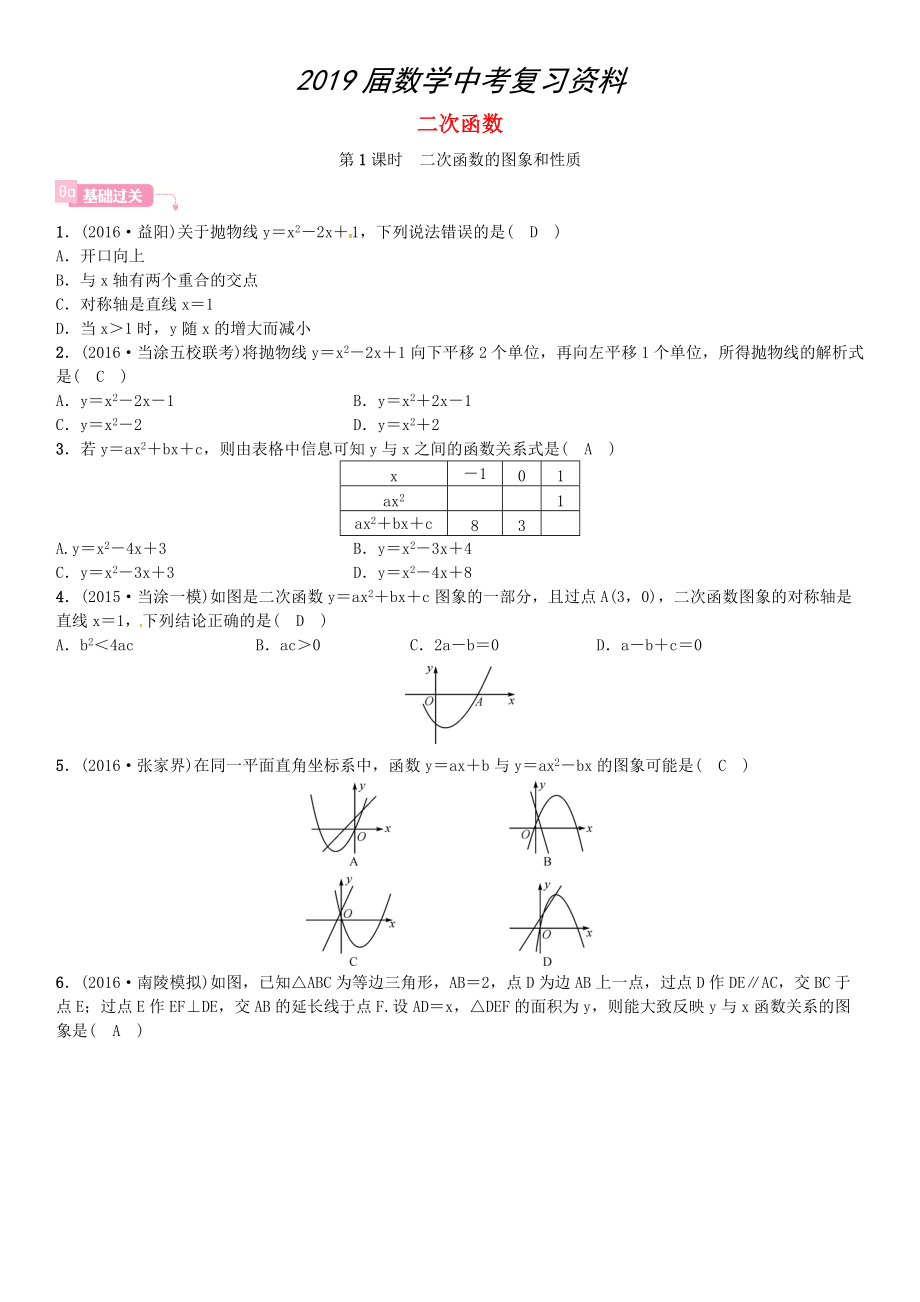
1.(2016益陽)關(guān)于拋物線y=x2-2x+1���,下列說法錯誤的是( D )
A.開口向上
B.與x軸有兩個重合的交點
C.對稱軸是直線x=1
D.當(dāng)x>1時,y隨x的增大而減小
2.(2016當(dāng)涂五校聯(lián)考)將拋物線y=x2-2x+1向下平移2個單位����,再向左平移1個單位,所得拋物線的解析式是( C )
A.y=x2-2x-1 B.y=x2+2x-1
C.y=x2-2 D.y=x2+2
3.
2����、若y=ax2+bx+c,則由表格中信息可知y與x之間的函數(shù)關(guān)系式是( A )
x
-1
0
1
ax2
1
ax2+bx+c
8
3
A.y=x2-4x+3 B.y=x2-3x+4
C.y=x2-3x+3 D.y=x2-4x+8
4.(2015當(dāng)涂一模)如圖是二次函數(shù)y=ax2+bx+c圖象的一部分���,且過點A(3��,0),二次函數(shù)圖象的對稱軸是直線x=1�,下列結(jié)論正確的是( D )
A.b2<4ac B.a(chǎn)c>0 C.
3、2a-b=0 D.a(chǎn)-b+c=0
5.(2016張家界)在同一平面直角坐標(biāo)系中,函數(shù)y=ax+b與y=ax2-bx的圖象可能是( C )
6.(2016南陵模擬)如圖�����,已知△ABC為等邊三角形�,AB=2,點D為邊AB上一點�����,過點D作DE∥AC����,交BC于點E;過點E作EF⊥DE��,交AB的延長線于點F.設(shè)AD=x��,△DEF的面積為y���,則能大致反映y與x函數(shù)關(guān)系的圖象是( A )
7.(2015懷化)二次函數(shù)y=x2+2x的頂點坐標(biāo)為(-1�����,-1)��,對稱軸是直線x=-1.
8.(2015馬鞍山期末)函數(shù)y=(x-2)(3-x)取得最大值時��,x=2.5
4����、.
9.(2016阜陽潁泉區(qū)一模)已知拋物線y=ax2+bx+c(c≠0)的對稱軸為直線x=1,且經(jīng)過點P(-1�,0),則拋物線與x軸的另一個交點坐標(biāo)為(3����,0).
10.已知拋物線y=ax2+bx+c(a>0)的對稱軸為直線x=1,且經(jīng)過點(-1�,y1),(-2�,y2),試比較y1和y2的大?��。簓1<y2(填“>”“<”或“=”).
11.(2016靈璧縣一模)已知二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示����,有下列5個結(jié)論:①c=0�;②該拋物線的對稱軸是直線x=-1;③當(dāng)x=1時��,y=2a;
④am2+bm+a>0(m≠-1)��;⑤設(shè)A(100��,y1)���,B(-100,y2)在
5��、該拋物線上�,則y1>y2.其中正確的結(jié)論有①②④⑤.(寫出所有正確結(jié)論的序號)
提示:拋物線與y軸交于原點,c=0���,故①正確���;該拋物線的對稱軸是直線x=-1,故②正確�;當(dāng)x=1時,y=a+b+c.∵對稱軸是直線x=-1�����,∴-=-1�,b=2a.又∵c=0��,∴y=3a.故③錯誤����;x=m對應(yīng)的函數(shù)值為y=am2+bm+c.x=-1對應(yīng)的函數(shù)值為y=a-b+c�,又∵x=-1時函數(shù)取得最小值,∴a-b+c<am2+bm+c��,即a-b<am2+bm.∵b=2a��,∴am2+bm+a>0(m≠-1).故④正確����;∵|100+1|>|-100+1|,且開口向上���,∴y1>y2.故⑤正確.
12.(20
6�、16安慶一模)已知拋物線C:y=x2-4x+3.
(1)求該拋物線關(guān)于y軸對稱的拋物線C1的解析式����;
(2)將拋物線C平移至C2,使其經(jīng)過點(1�����,4).若頂點在x軸上,求C2的解析式.
解:(1)y=x2-4x+3=(x-2)2-1.
∴拋物線C頂點坐標(biāo)是(2���,-1)����,與y軸交點坐標(biāo)是(0����,3).
∵C1與C關(guān)于y軸對稱�,
∴C1頂點坐標(biāo)是(-2,-1)��,且與y軸交點坐標(biāo)是(0����,3).
設(shè)C1的解析式為y=a(x+2)2-1,
把(0����,3)代入,解得a=1.
∴C1的解析式為y=x2+4x+3.
(2)設(shè)平移后拋物線的解析式為y=(x-h(huán))2.
∵拋物線C2經(jīng)過點(1�����,
7、4)�,
∴(1-h(huán))2=4,解得h=-1或h=3.
∴C2的解析式為y=(x+1)2或y=(x-3)2��,
即y=x2+2x+1或y=x2-6x+9.
13.(2016寧波)如圖���,已知拋物線y=-x2+mx+3與x軸交于A����,B兩點��,與y軸交于點C���,點B的坐標(biāo)為(3�����,0).
(1)求m的值及拋物線的頂點坐標(biāo)����;
(2)點P是拋物線對稱軸l上的一個動點�����,當(dāng)PA+PC的值最小時,求點P的坐標(biāo).
解:(1)把點B的坐標(biāo)為(3����,0)代入拋物線y=-x2+mx+3,得0=-32+3m+3���,解得m=2.
∴y=-x2+2x+3=-(x-1)2+4.
∴頂點坐標(biāo)為(1����,4).
(
8���、2)連接BC交拋物線對稱軸l于點P,則此時PA+PC的值最?���。?
設(shè)直線BC的解析式為y=kx+b.
∵點C(0,3)�,點B(3,0)���,
∴ 解得
∴直線BC的解析式為y=-x+3.
當(dāng)x=1時�,y=-1+3=2.
∴當(dāng)PA+PC的值最小時����,點P的坐標(biāo)為(1�����,2).
14.(2016合肥十校聯(lián)考一)已知二次函數(shù)y=a(x-2)2+c��,當(dāng)x=x1時���,函數(shù)值為y1;當(dāng)x=x2時��,函數(shù)值為y2�����,若|x1-2|>|x2-2|��,則下列表達(dá)式正確的是( C )
A.y1+y2>0 B.y1-y2>0
C.a(chǎn)(y1-y2)>0
9���、 D.a(chǎn)(y1+y2)>0
15.(2015資陽)已知拋物線p:y=ax2+bx+c的頂點為C�,與x軸相交于A�,B兩點(點A在點B左側(cè)),點C關(guān)于x軸的對稱點為C′,我們稱以A為頂點且過點C′����,對稱軸與y軸平行的拋物線為拋物線p的“夢之星”拋物線,直線AC′為拋物線p的“夢之星”直線.若一條拋物線的“夢之星”拋物線和“夢之星”直線分別是y=x2+2x+1和y=2x+2�����,則這條拋物線的解析式為y=x2-2x-3.
16.(2016合肥十校聯(lián)考二)在平面直角坐標(biāo)系中�,已知拋物線y=x2+bx+c與x軸交于點A(-1,0)和點B��,與y軸交于點C(0�,-2).
(1
10、)求該拋物線的表達(dá)式����,并寫出其對稱軸���;
(2)點D為該拋物線的頂點�,設(shè)點E(m��,0)(m>2)����,如果△BDE和△CDE的面積相等����,求E點坐標(biāo).
解:(1)∵拋物線y=x2+bx+c經(jīng)過點A(-1�����,0)�,C(0,-2)���,
∴ 解得
∴拋物線的表達(dá)式為y=x2-x-2�����,對稱軸為直線x=.
(2)由(1)知���,拋物線的表達(dá)式為y=x2-x-2=(x-)2-,∴點D(����,-).
當(dāng)y=x2-x-2=0時,x1=-1�,x2=2���,
∴點B(2,0).
若△BDE和△CDE的面積相等��,則DE∥BC.
∵直線BC的解析式為y=x-2�,
∴直線DE的解析式為y=x-.
當(dāng)y=0時,m=��,∴E
11���、(�����,0).
17.(2015安慶二模)如圖所示�����,二次函數(shù)y=-2x2+4x+m的圖象與x軸的一個交點為A(3�����,0),另一個交點為B���,且與y軸交于點C.
(1)求m的值及點B的坐標(biāo)���;
(2)求△ABC的面積����;
(3)該二次函數(shù)圖象上有一點D(x���,y)��,使S△ABD=S△ABC��,請求出D點的坐標(biāo).
解:(1) ∵ 函數(shù)過A(3����,0)�����,
∴ -18+12+m=0���,即m=6.
∴ 該函數(shù)解析式為y=-2x2+4x+6.
又∵當(dāng)-2x2+4x+6=0時�,x1=-1�,x2=3�,
∴點B的坐標(biāo)為(-1����,0) .
(2)C點坐標(biāo)為(0,6)���,S△ABC==12.
(3)∵S△A
12����、BD=S△ABC=12�,
∴S△ABD=12.
∴S△ABD==12.∴|h|=6.
①當(dāng)h=6時,-2x2+4x+6=6�,
解得x1=0,x2=2.
∴D點坐標(biāo)為(2���,6)����;
②當(dāng)h=-6時�����,-2x2+4x+6=-6��,
解得x1=1+�����,x2=1-.
∴D點坐標(biāo)為(1+���,-6)�����,(1-��,-6).
綜上所述��,D點坐標(biāo)為(2����,6)���,(1+�,-6) �����,(1-,-6) .
18.(2016荊州)若函數(shù)y=(a-1)x2-4x+2a的圖象與x軸有且只有一個交點�����,則a的值為-1或2或1.
提示:分2種情況:①當(dāng)y是x的一次函數(shù)時�,a-1=0,即a=1����;②當(dāng)y是x的二次函數(shù)時,a≠1�����,且Δ=(-4)2-4(a-1)2a=0�,解得a=-1或2.
 安徽省中考數(shù)學(xué)總復(fù)習(xí) 第一輪 考點系統(tǒng)復(fù)習(xí) 第三單元 函數(shù) 第12講 二次函數(shù) 第1課時 二次函數(shù)的圖象和性質(zhì)試題
安徽省中考數(shù)學(xué)總復(fù)習(xí) 第一輪 考點系統(tǒng)復(fù)習(xí) 第三單元 函數(shù) 第12講 二次函數(shù) 第1課時 二次函數(shù)的圖象和性質(zhì)試題