《2015高中數(shù)學(xué) 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3》由會(huì)員分享���,可在線閱讀�����,更多相關(guān)《2015高中數(shù)學(xué) 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索��。
1���、2. 3變量間的相關(guān)關(guān)系(講)
一�����、相關(guān)關(guān)系:
自變量取值一定時(shí)���,因變量的取值帶有一定隨機(jī)性的兩個(gè)變量之間的關(guān)系,叫做相關(guān)關(guān)系��。
【說明】函數(shù)關(guān)系是一種非常確定的關(guān)系�,而相關(guān)關(guān)系是一種非確定性關(guān)系。
思考探究:
1���、有關(guān)法律規(guī)定�����,香煙盒上必須印上“吸煙有害健康”的警示語����。吸煙是否一定會(huì)引起健康問題?你認(rèn)為“健康問題不一定是由吸煙引起的,所以可以吸煙”的說法對嗎�?
2、某地區(qū)的環(huán)境條件適合天鵝棲息繁衍�����,有人經(jīng)統(tǒng)計(jì)發(fā)現(xiàn)了一個(gè)有趣的現(xiàn)象���,如果村莊附近棲息的天鵝多,那么這個(gè)村莊的嬰兒出生率也高����,天鵝少的地方嬰兒出生率低,于是他得出了一個(gè)結(jié)論:天鵝能夠帶來孩子���。你認(rèn)為這樣的結(jié)論可靠嗎����?如何證
2����、明這個(gè)問題的可靠性?
分析:(1)吸煙只是影響健康的一個(gè)因素���,對健康的影響還有其他的一些因素�����,兩者之間非函數(shù)關(guān)系即非因果關(guān)系��;
(2)不對�����,這也是相關(guān)關(guān)系而不是函數(shù)關(guān)系���。
上面提到了很多相關(guān)關(guān)系���,那它們之間的相關(guān)關(guān)系強(qiáng)還是弱?我們下面來研究一下��。
二���、散點(diǎn)圖
探究:在一次對人體脂肪含量和年齡關(guān)系的研究中����,研究人員獲得了一組樣本數(shù)據(jù):
年齡
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
3����、
年齡
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
其中各年齡對應(yīng)的脂肪數(shù)據(jù)是這個(gè)年齡人群脂肪含量的樣本平均數(shù)����。
思考探究:
1�����、對某一個(gè)人來說����,他的體內(nèi)脂肪含量不一定隨年齡增長而增加或減少�,但是如果把很多個(gè)體放在一起,就可能
4��、表現(xiàn)出一定的規(guī)律性.觀察上表中的數(shù)據(jù)����,大體上看,隨著年齡的增加�,人體脂肪含量怎樣變化?
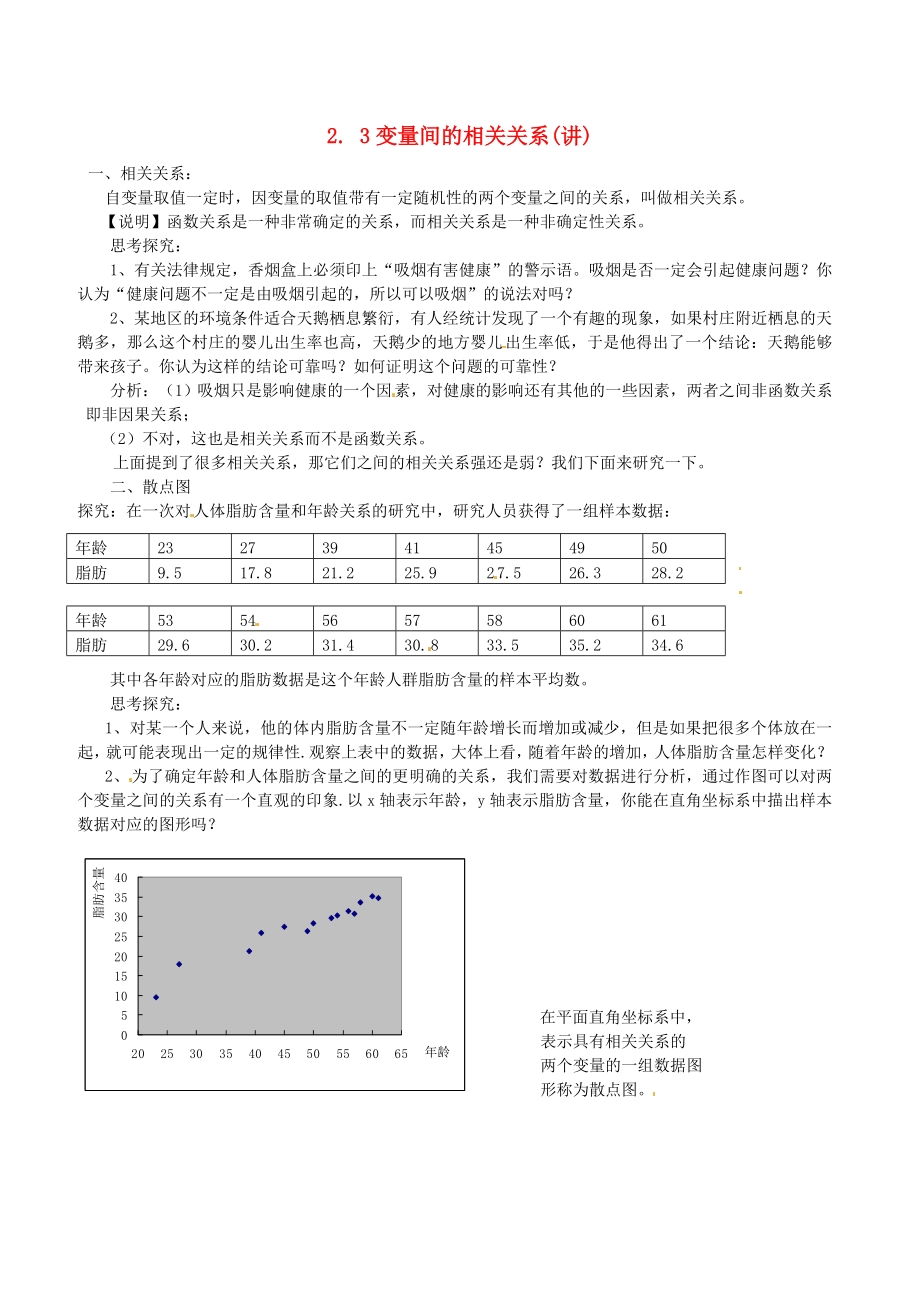
2���、為了確定年齡和人體脂肪含量之間的更明確的關(guān)系�,我們需要對數(shù)據(jù)進(jìn)行分析,通過作圖可以對兩個(gè)變量之間的關(guān)系有一個(gè)直觀的印象.以x軸表示年齡�,y軸表示脂肪含量,你能在直角坐標(biāo)系中描出樣本數(shù)據(jù)對應(yīng)的圖形嗎��?
在平面直角坐標(biāo)系中����,
表示具有相關(guān)關(guān)系的
兩個(gè)變量的一組數(shù)據(jù)圖
形稱為散點(diǎn)圖。
3��、觀察人的年齡的與人體脂肪含量散點(diǎn)圖
5��、的大致趨勢����,有什么樣的特點(diǎn)?閱讀課本��,這種相關(guān)關(guān)系我們稱為什么�?還有沒有其他的相關(guān)關(guān)系?它又有怎樣的特點(diǎn)���?
三����、線性相關(guān)、回歸直線方程和最小二乘法
在各種各樣的散點(diǎn)圖中��,有些散點(diǎn)圖中的點(diǎn)是雜亂分布的����,有些散點(diǎn)圖中的點(diǎn)的分布有一定的規(guī)律性,年齡和人體脂肪含量的樣本數(shù)據(jù)的散點(diǎn)圖中的點(diǎn)的分布有什么特點(diǎn)���?
如果散點(diǎn)圖中的點(diǎn)的分布,從整體上看大致在一條直線附近�,則稱這兩個(gè)變量之間具有線性相關(guān)關(guān)系,這條直線叫做回歸直線��。
我們所畫的回歸直線應(yīng)該使散點(diǎn)圖中的各點(diǎn)在整體上盡可能的與其接近����。我們怎么來實(shí)現(xiàn)這一目的呢?說一說你的想法���。
設(shè)所求的直線方程為=bx+a����,其中a�、b是待定系數(shù)��。
則i=bx
6��、i+a(i=1����,2����,…,n).于是得到各個(gè)偏差
yi-i =yi-(bxi+a)(i=1��,2�����,…�����,n)
顯見�,偏差yi-i 的符號(hào)有正有負(fù),若將它們相加會(huì)造成相互抵消��,所以它們的和不能代表幾個(gè)點(diǎn)與相應(yīng)直線在整體上的接近程度����,故采用n個(gè)偏差的平方和
Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2
表示n個(gè)點(diǎn)與相應(yīng)直線在整體上的接近程度��。
記Q=
這樣��,問題就歸結(jié)為:當(dāng)a����、b取什么值時(shí)Q最小����,a、b的值由下面的公式給出:
其中=�����,=���,a為回歸方程的斜率,b為截距����。
求回歸直線,使得樣本數(shù)據(jù)的點(diǎn)到它的距離的平方和最小的方法叫最小二乘法����。
【例題精
7����、析】
有一個(gè)同學(xué)家開了一個(gè)小賣部���,他為了研究氣溫對熱飲銷售的影響����,經(jīng)過統(tǒng)計(jì)����,得到一個(gè)賣出的飲料杯數(shù)與當(dāng)天氣溫的對比表:
攝氏溫度
-5
0
4
7
12
15
19
23
27
31
36
熱飲杯數(shù)
156
150
132
128
130
116
104
89
93
76
54
(1)畫出散點(diǎn)圖;
(2)從散點(diǎn)圖中發(fā)現(xiàn)氣溫與熱飲杯數(shù)之間關(guān)系的一般規(guī)律�����;
(3)求回歸方程�;
(4)如果某天的氣溫是2℃,預(yù)測這天賣出的熱飲杯數(shù)���。
解:
(4)當(dāng)x=2時(shí)�,y=143.063
反思總結(jié)��,當(dāng)堂檢測。
1���、求樣本數(shù)據(jù)的線性回歸方程����,可按下列步驟進(jìn)行:
(1)計(jì)算平均數(shù)��,�����;
(2)求a�����,b�����;
(3)寫出回歸直線方程���。
2、回歸方程被樣本數(shù)據(jù)惟一確定�����,對同一個(gè)總體,不同的樣本數(shù)據(jù)對應(yīng)不同的回歸直線�����,所以回歸直線也具有隨機(jī)性.�。
3、對于任意一組樣本數(shù)據(jù)�����,利用上述公式都可以求得“回歸方程”����,如果這組數(shù)據(jù)不具線性相關(guān)關(guān)系,即不存在回歸直線����,那么所得的“回歸方程”是沒有實(shí)際意義的。因此���,對一組樣本數(shù)據(jù)����,應(yīng)先作散點(diǎn)圖,在具有線性相關(guān)關(guān)系的前提下再求回歸方程
 2015高中數(shù)學(xué) 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3
2015高中數(shù)學(xué) 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3