2022年高考數(shù)學總復習 第四章4.2 同角三角函數(shù)的基本關系及三角函數(shù)的誘導公式教案 理 北師大版

《2022年高考數(shù)學總復習 第四章4.2 同角三角函數(shù)的基本關系及三角函數(shù)的誘導公式教案 理 北師大版》由會員分享，可在線閱讀，更多相關《2022年高考數(shù)學總復習 第四章4.2 同角三角函數(shù)的基本關系及三角函數(shù)的誘導公式教案 理 北師大版（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。

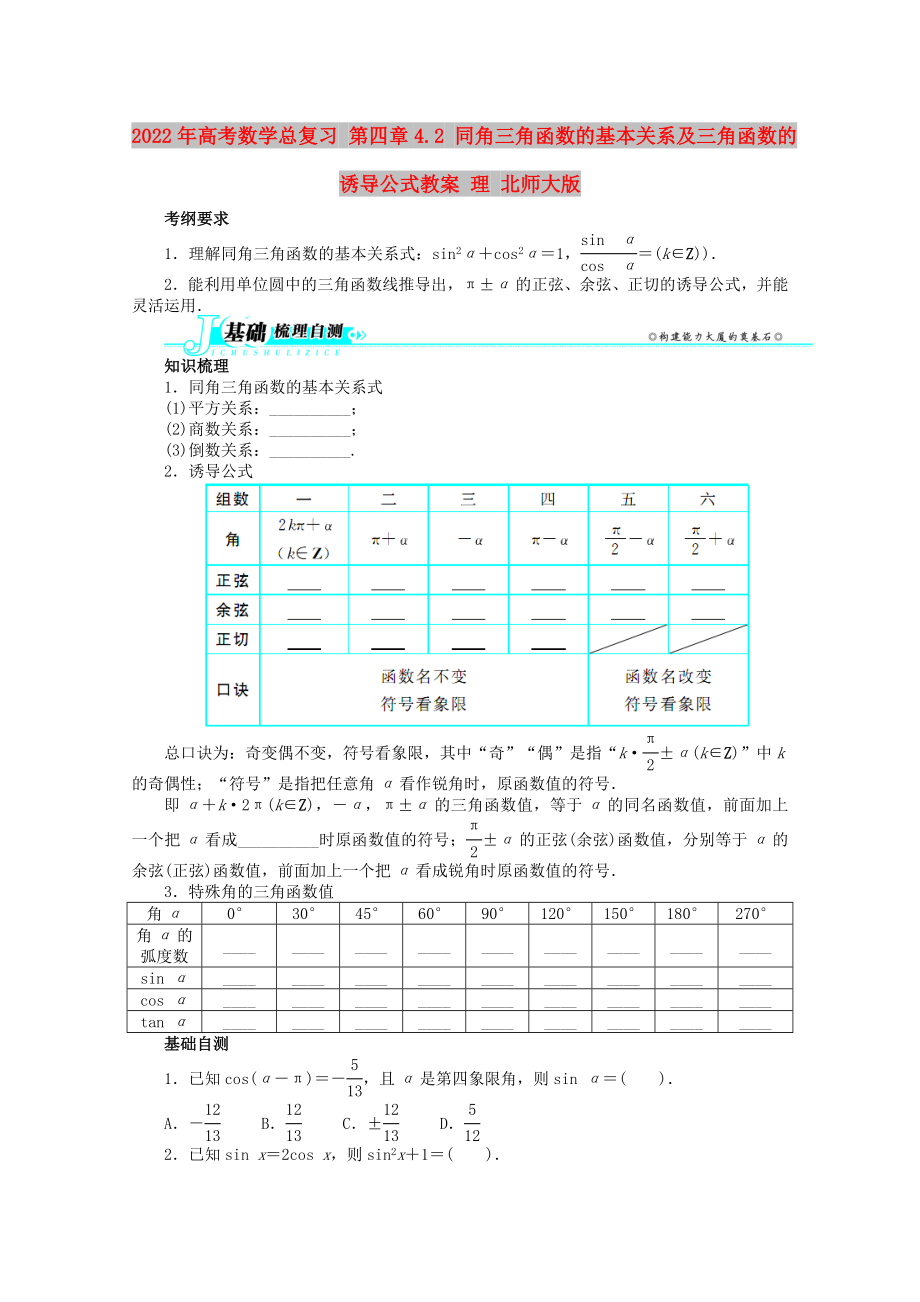
1、2022年高考數(shù)學總復習 第四章4.2 同角三角函數(shù)的基本關系及三角函數(shù)的誘導公式教案 理 北師大版 考綱要求 1．理解同角三角函數(shù)的基本關系式：sin2α＋cos2α＝1，＝(k∈Z))． 2．能利用單位圓中的三角函數(shù)線推導出，π±α的正弦、余弦、正切的誘導公式，并能靈活運用． 知識梳理 1．同角三角函數(shù)的基本關系式 (1)平方關系：__________； (2)商數(shù)關系：__________； (3)倒數(shù)關系：__________. 2．誘導公式 總口訣為：奇變偶不變，符號看象限，其中“奇”“偶”是指“k·±α(k∈Z)”中k的奇偶性；“符號”是指把任意角α看作

2、銳角時，原函數(shù)值的符號． 即α＋k·2π(k∈Z)，－α，π±α的三角函數(shù)值，等于α的同名函數(shù)值，前面加上一個把α看成__________時原函數(shù)值的符號；±α的正弦(余弦)函數(shù)值，分別等于α的余弦(正弦)函數(shù)值，前面加上一個把α看成銳角時原函數(shù)值的符號． 3．特殊角的三角函數(shù)值 角α 0° 30° 45° 60° 90° 120° 150° 180° 270° 角α的 弧度數(shù) ____ ____ ____ ____ ____ ____ ____ ____ ____ sin α ____ ____ ____ ____ ____ ___

3、_ ____ ____ ____ cos α ____ ____ ____ ____ ____ ____ ____ ____ ____ tan α ____ ____ ____ ____ ____ ____ ____ ____ ____ 基礎自測 1．已知cos(α－π)＝－，且α是第四象限角，則sin α＝(　　)． A．－ B． C．± D． 2．已知sin x＝2cos x，則sin2x＋1＝(　　)． A． B． C． D． 3．已知α是第四象限角，tan α＝－，則sin α等于

4、(　　)． A． B．－ C． D．－ 4．已知＝5，則sin2α－sin αcos α的值是________． 思維拓展 1．有人說sin(kπ－α)＝sin(π－α)＝sin α(k∈Z)，你認為正確嗎？ 提示：不正確．當k＝2n(n∈Z)時，sin(kπ－α)＝sin(2nπ－α)＝sin(－α)＝－sin α； 當k＝2n＋1(n∈Z)時，sin(kπ－α)＝sin[(2n＋1)·π－α]＝sin(2nπ＋π－α)＝sin(π－α)＝sin α. 2．“符號看象限”中，符號是否與α的大小有關？ 提示：無關，只是把α從形式上看作銳角，從而2kπ＋α

5、(k∈Z)，π＋α，－α，π－α，－α，＋α分別是第一，三，四，二，一，二象限的角． 一、同角三角函數(shù)關系式的應用 【例1－1】已知tan α＝，則cos 2α＋sin2α的值為__________． 【例1－2】已知α是三角形的內(nèi)角，且sin α＋cos α＝. (1)求tan α的值； (2)把用tan α表示出來，并求其值． 方法提煉1．利用sin2α＋cos2α＝1可以實現(xiàn)角α的正弦、余弦的互化，利用＝tan α可以實現(xiàn)角α的弦切互化． 2．注意公式逆用及變形應用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α. 請做[針對訓練]

6、1 二、誘導公式的應用 【例2－1】化簡：··＝__________. 【例2－2】化簡：＋. 【例2－3】已知cos(π＋α)＝－，且α是第四象限角，計算：(n∈Z)． 方法提煉利用誘導公式化簡求值時的原則為： 1．“負化正”，運用公式三將任意負角的三角函數(shù)化為任意正角的三角函數(shù)． 2．“大化小”，利用公式一將大于360°的角的三角函數(shù)化為0°到360°的三角函數(shù)，利用公式二將大于180°的角的三角函數(shù)化為0°到180°的三角函數(shù)． 3．“小化銳”，利用公式六將大于90°的角化為0°到90°的角的三角函數(shù)． 4．“銳求值”，得到0°到90°的三角函數(shù)后，若是特殊角直接求得，

7、若是非特殊角可由計算器求得． 請做[針對訓練]2 三、sin x±cos x與方程思想 【例3】已知sin θ－cos θ＝，求： (1)sin θcos θ；(2)sin3θ－cos3θ；(3)sin4θ＋cos4θ. 方法提煉1．已知asin x＋bcos x＝c可與sin2x＋cos2x＝1聯(lián)立，求得sin x，cos x，一般此法不常用，原因是計算麻煩． 2．sin x＋cos x，sin x－cos x，sin xcos x之間的關系為： (sin x＋cos x)2＝1＋2sin xcos x， (sin x－cos x)2＝1－2sin xcos x， (sin

8、 x＋cos x)2＋(sin x－cos x)2＝2. 因此已知上述三個代數(shù)式中的任意一個代數(shù)式的值可求其余兩個代數(shù)式的值． 請做[針對訓練]3 考情分析 從近幾年的高考試題來看，同角三角函數(shù)的基本關系和誘導公式中是高考的熱點，題型既有選擇題、填空題，又有解答題．主要考查誘導公式在三角函數(shù)式求值，化簡的過程中與同角三角函數(shù)的關系式，和差角公式及倍角公式的綜合應用，在考查基本運算的同時，注重考查等價轉(zhuǎn)化的思想方法． 預測xx年高考仍將以誘導公式為主要考點，重點考查考生的運算能力與恒等變形能力． 針對訓練 1．(xx重慶高考，文12)若cos α＝－，且α∈，則tan α＝__

9、________. 2．已知A＝＋(k∈Z)，則A的值構成的集合是__________． 3．已知關于x的方程2x2－(＋1)x＋m＝0的兩根為sin θ和cos θ，θ∈(0,2π)，求m的值． 參考答案 基礎梳理自測 知識梳理 1．(1)sin2α＋cos2α＝1　(2)tan α＝　(3)tan α·cot α＝1 2．sin α?。璼in α　－sin α　sin α　cos α cos α　cos α?。璫os α　cos α?。璫os α　sin α －sin α　tan α　tan α　－tan α?。璽an α　銳角 3．0　　　　　　π π　　0　　　　

10、1　　 0?。?　1　　　　0?。? －?。?　0　0　　1　　不存在　－?。?　不存在 基礎自測 1．A　解析：cos(α－π)＝－cos α＝－，cos α＝. sin α＝±＝±， ∵α是第四象限角，∴sin α＝－. 2．B　解析：∵sin2x＋cos2x＝1， ∴sin2x＋2＝1，∴sin2x＝，∴sin2x＋1＝. 3．D　解析：由tan α＝＝－，sin2α＋cos2α＝1及α是第四象限角，解得sin α＝－. 4．　解析：由＝5得，＝5，即tan α＝2. 所以sin2α－sin αcos α＝ ＝＝. 考點探究突破 【例1－1】　解析：cos 2

11、α＋sin2α ＝1－2sin2α＋sin2α＝cos2α ＝＝＝. 【例1－2】解：(1)聯(lián)立方程 由①得cos α＝－sin α，將其代入②. 整理得25sin2α－5sin α－12＝0. ∵α是三角形的內(nèi)角， ∴∴tan α＝－. (2)＝＝＝.∵tan α＝－， ∴＝＝＝－. 【例2－1】sin x　解析：原式＝··＝·tan x·tan x＝sin x. 【例2－2】解：原式＝＋＝＋＝. 【例2－3】解：∵cos(π＋α)＝－. ∴－cos α＝－，cos α＝. 則 ＝ ＝ ＝＝ ＝－＝－4. 【例3】解：(1)∵sin θ－cos θ＝

12、， ∴(sin θ－cos θ)2＝， 即sin2θ－2sin θcos θ＋cos2θ＝. 由平方關系sin2θ＋cos2θ＝1，可得sin θcos θ＝. (2)sin3θ－cos3θ＝(sin θ－cos θ)(sin2θ＋cos θsin θ＋cos2θ)． 由平方關系及sin θ－cos θ＝，可得sin3θ－cos3θ＝×＝. (3)由(sin2θ＋cos2θ)2＝sin4θ＋2sin2θ·cos2θ＋cos4θ＝1， 可得sin4θ＋cos4θ＝1－2sin2θ·cos2θ＝1－2×＝. 演練鞏固提升 針對訓練 1．　解析：由1＋tan2α＝，則tan2α＝.又因α∈，故tan α＞0，則tan α＝. 2．{－2,2}　解析：當k為偶數(shù)時，A＝＋＝2；k為奇數(shù)時，A＝－＝－2. 3．解：由韋達定理可知 由①式平方得1＋2sin θcos θ＝， ∴sin θcos θ＝，由②得＝. ∴m＝.