《課程設(shè)計(jì) 家家學(xué)教育 小學(xué)六年級 數(shù)學(xué)專項(xiàng)訓(xùn)練 數(shù)學(xué) 幾何》由會員分享�,可在線閱讀,更多相關(guān)《課程設(shè)計(jì) 家家學(xué)教育 小學(xué)六年級 數(shù)學(xué)專項(xiàng)訓(xùn)練 數(shù)學(xué) 幾何(10頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�����。
1�、
生活就像海洋,只有意志堅(jiān)強(qiáng)的人����,才能到達(dá)彼岸馬克思
第二講
幾何
真題模考
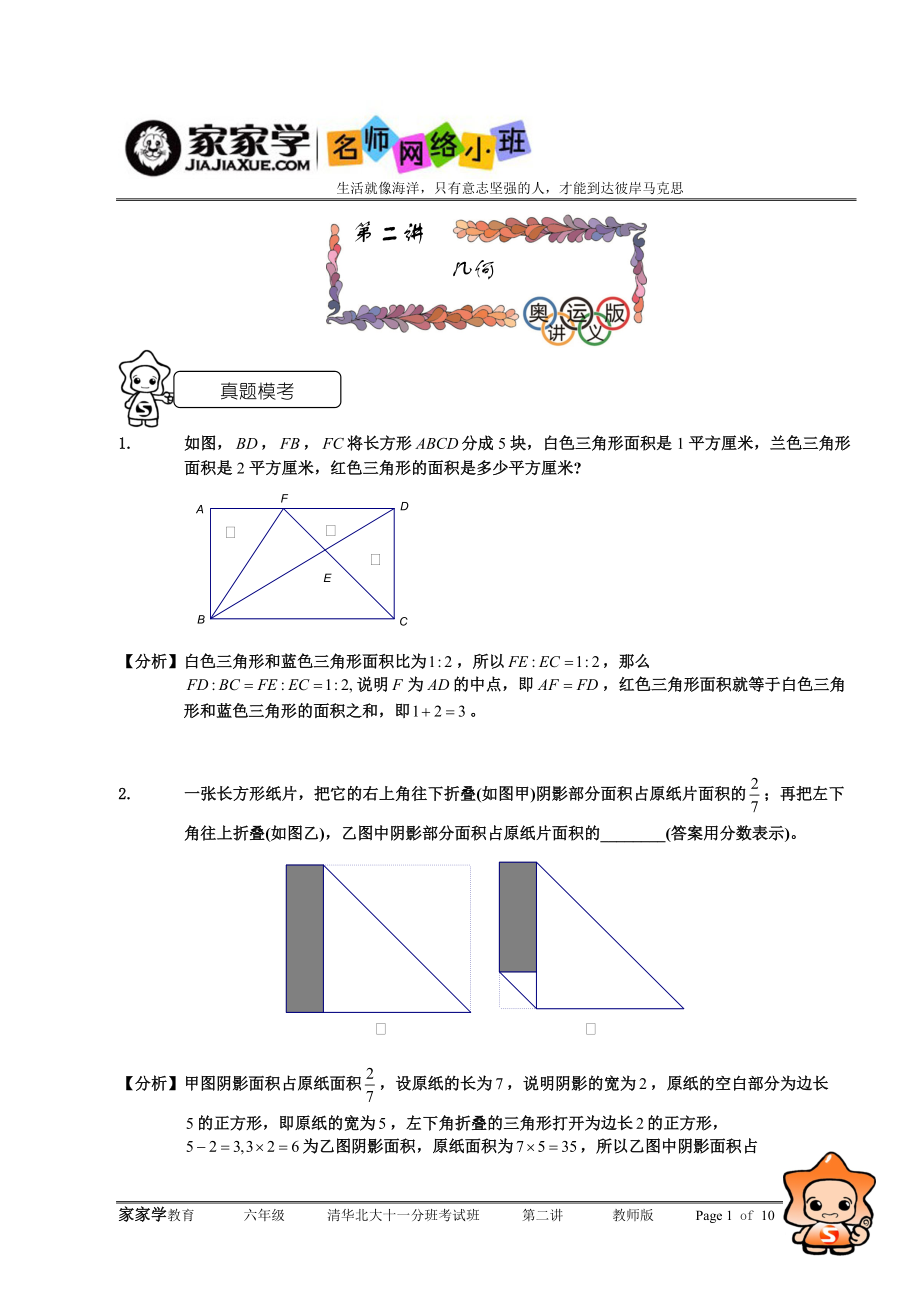
1. 如圖�,,�,將長方形分成5塊,白色三角形面積是1平方厘米�����,蘭色三角形面積是2平方厘米��,紅色三角形的面積是多少平方厘米?
【分析】白色三角形和藍(lán)色三角形面積比為�����,所以���,那么 說明為的中點(diǎn)��,即��,紅色三角形面積就等于白色三角形和藍(lán)色三角形的面積之和��,即�����。
2. 一張長方形紙片�,把它的右上角往下折疊(如圖甲)陰影部分面積占原紙片面積的;再把左下角往上折疊(如圖乙)��,乙圖中陰影部分面積占原紙片面積的________(答案用分?jǐn)?shù)表示)�。
【分析】甲圖陰
2、影面積占原紙面積���,設(shè)原紙的長為���,說明陰影的寬為,原紙的空白部分為邊長的正方形���,即原紙的寬為����,左下角折疊的三角形打開為邊長的正方形����,為乙圖陰影面積,原紙面積為��,所以乙圖中陰影面積占原紙面積的。
3. 有甲����、乙、丙三個(gè)梯形����,他們的高之比是�����,上底之比依次是�,下底之比依次是.已知甲梯形的面積是平方厘米,那么乙與丙兩個(gè)梯形的面積之和是多少平方厘米?
【分析】 設(shè)甲梯形的高為�,上底的長為,下底的長為�,那么根據(jù)甲梯形的面積公式得到等式:
,整理為���,而乙梯形的面積為���,丙梯形的面積為,乙丙兩個(gè)梯形的面積之和為
=平方厘米�����。
4. 如圖,是47的長方形��,是210長方形�,那么,三角
3����、形形的面積與的面積之差是_______。
【分析】
又
���。
5. 如圖����,正方形的面積是120平方厘米�,是的中點(diǎn),是的中點(diǎn)��,四邊形的面積是 平方厘米.
【分析】
即
���。
6. 一個(gè)圓柱體底面周長和高相等.如果高縮短4厘米���,表面積就減少50.24平方厘米.求這個(gè)圓柱體的表面積是多少�?
【分析】(如圖)一個(gè)圓柱體底面周長和高相等����,說明圓柱體側(cè)面展開
4、是一個(gè)正方體.高縮短厘米�����,表面積就減少平方厘米.陰影部分的面積為圓柱體表面積減少部分����,值是平方厘米��,所以底面周長是 (厘米)側(cè)面積是:
(平方厘米)
兩個(gè)底面積是: (平方厘米)����。
表面積:(平方厘米)。
7. 在一個(gè)底面半徑為4厘米�����,高為20厘米的圓柱形水杯內(nèi)裝滿了水���,另有一個(gè)圓錐形空水杯.它的上口周長為62.8厘米���,現(xiàn)把圓柱形水杯里的水往圓錐形水杯里倒�,當(dāng)圓錐形水杯裝滿時(shí).圓柱形水杯中還剩下14厘米高的水�����,求圓錐形水杯的高?
【分析】 設(shè)圓錐高�����,
��,
�,
。
5���、8. 如圖���,是等腰直角三角形,是圓周的中點(diǎn)�����,是半圓的直徑��,已知厘米,求陰影面積�。
【分析】設(shè)交于,
陰影面積
9. 如圖相鄰兩個(gè)格點(diǎn)間的距離是1�����,則圖中陰影三角形的面積為________���。
【分析】連接��,
則可根據(jù)格點(diǎn)面積公式�,可以得到的面積=
的面積=
所以=����,所以��。
10. 下圖中陰影部分的面積是 �����。
【分析】
�����。
考點(diǎn)拓展
【例1】 雨嘩嘩地下個(gè)不停.在雨地里放一個(gè)(如圖1)
6、那樣的圓柱體容器.(單位:厘米)雨水將它下滿要用1時(shí).有����、、三種下同的容器���,請問哪個(gè)容器最先接滿雨水.
【分析】 根據(jù)題意知雨均勻地下.即單位面積內(nèi)的降雨量相同.所以雨下滿某容器所需的時(shí)間與該容器的容積和接水面(敞開部分)的面積之比有關(guān).
容器:需小時(shí)�����;
容器:需小時(shí)��;
容器: 需小時(shí)����。
【例2】 如圖����,長方形的面積是,是的三等分點(diǎn)�����,,則陰影部分的面積為_____.
【分析】(解一)設(shè)交于�,交于,連接�。
(解二)設(shè)交于,交于��,的高�����,的高����,
,
���,
7����、 ����,
�����。
【例3】 在梯形中,和平行�����,且�。點(diǎn)、分別是和的中點(diǎn)��,已知陰影四邊形的面積是18�,求梯形面積是多少?
【分析】因?yàn)辄c(diǎn)����、分別是和的中點(diǎn),所以���,并且上下兩個(gè)小梯形的高相等��,設(shè)梯形和的高都是�����,設(shè)�����,則�����,�����,
三角形的上的高等于�,
三角形的上的高等于,
所以陰影部分的面積等于��,則����,解得,
梯形面積等于�。
【例4】 已知圖中每個(gè)正六邊形的面積是l,圖中虛線圍成五邊形的面積是 ���;
【分析】虛線外的圖形等于三個(gè)正六邊形加上兩個(gè)正六邊形的角��,
8、
即;
所以五變形的面積是�。
【例5】 如圖,長方形中��,����、分別為、邊上的點(diǎn)�,,���,求��。
【分析】作����,���,
設(shè)��,
則�;
���。
【例6】 如下圖兩個(gè)相同的正方形�,左圖中陰影部分是9個(gè)圓,右圖中陰影部分是16個(gè)圓.哪個(gè)圖中陰影部分的面積大?為什么?
【分析】設(shè)正方形邊長為�,每一個(gè)圓的半徑為,
說明陰影面積只與正方形的邊長有關(guān)系��,與圓的半徑無關(guān)�����,無論圓的半徑怎樣變化��,
只要正方形的邊長不變了�����,那么陰影面積就不變了��。
兩圖陰影面積相等����。
9、
課后練習(xí)
1. 有兩個(gè)邊長為厘米的正方體盒子�����,盒中放入直徑為厘米、高為8厘米的圓柱體鐵塊一個(gè)��,盒中放入直徑為4厘米���、高為8厘米的圓柱體鐵塊4個(gè),現(xiàn)在盒注滿水���,把盒的水倒入盒.使盒也注滿水����,問盒余下的水是多少立方厘米?
【分析】
2. 圓柱體的表面積是2512平方厘米�����,底面半徑是10厘米.這個(gè)圓柱體的體積是多少立方厘米?
【分析】設(shè)高為�,
圓柱體的體積為立方厘米。
3. 如下圖���,長方形和長方形拼成了長方形��,長方形的長是20�����,寬是12�,則它內(nèi)部陰影部分的面積是 。
【分析】陰影面積與空白面積相等����,為長方形面積一半。
4. 如圖���,每個(gè)小方格的邊長都是1���,求三角形的面積。
【分析】 因?yàn)?���,且,所以����,?
家家學(xué)教育 六年級 清華北大十一分班考試班 第二講 教師版 Page 10 of 10
 課程設(shè)計(jì) 家家學(xué)教育 小學(xué)六年級 數(shù)學(xué)專項(xiàng)訓(xùn)練 數(shù)學(xué) 幾何
課程設(shè)計(jì) 家家學(xué)教育 小學(xué)六年級 數(shù)學(xué)專項(xiàng)訓(xùn)練 數(shù)學(xué) 幾何