《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 第六章 圓 第二節(jié) 與圓有關(guān)的位置關(guān)系練習(xí)》由會(huì)員分享�����,可在線閱讀���,更多相關(guān)《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 第六章 圓 第二節(jié) 與圓有關(guān)的位置關(guān)系練習(xí)(9頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1�����、
第二節(jié) 與圓有關(guān)的位置關(guān)系
1.已知⊙O的半徑為3,圓心O到直線l的距離為2���,則直線l與⊙O的位置關(guān)系是( )
A.相交 B.相切
C.相離 D.不能確定
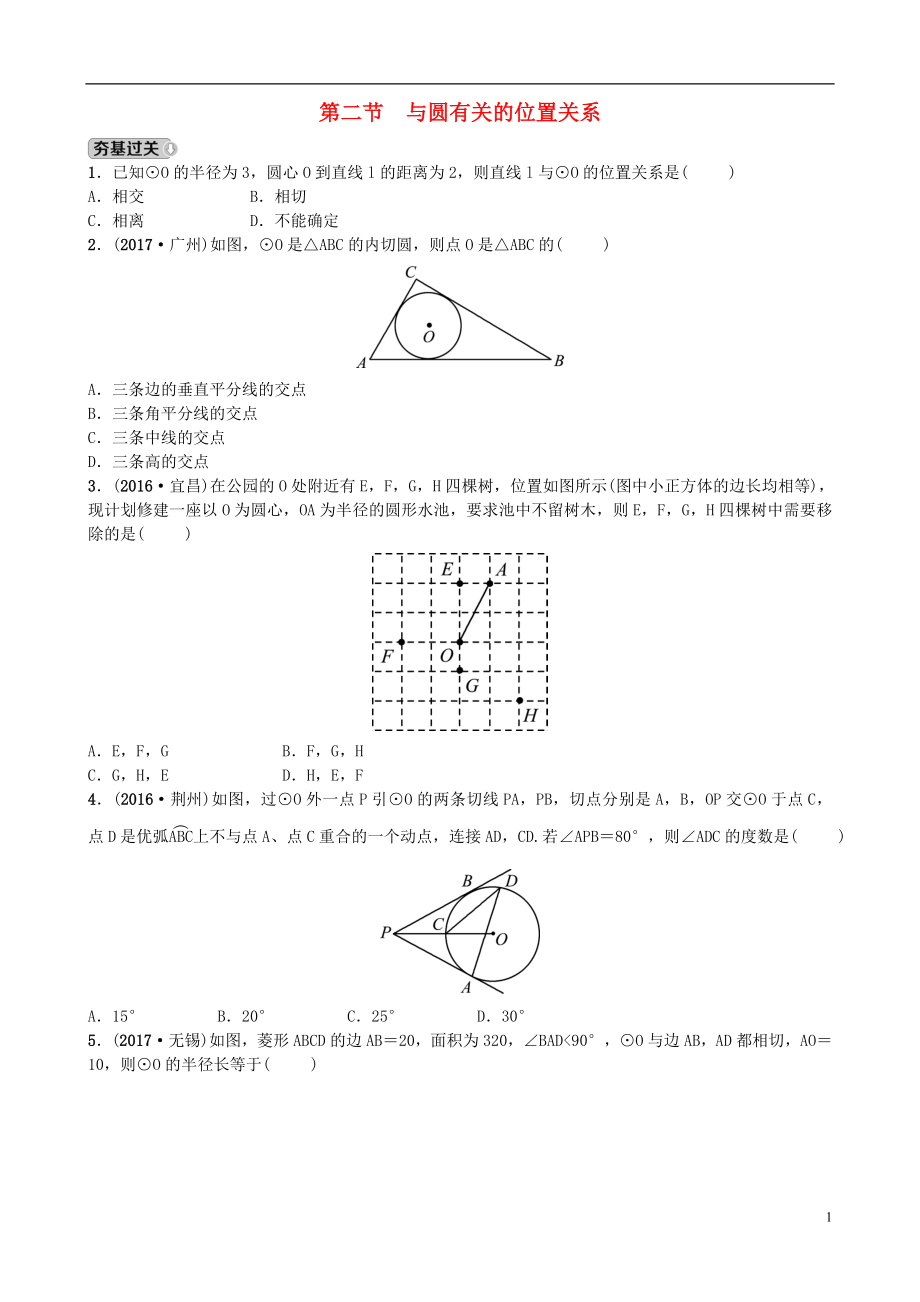
2.(2017·廣州)如圖,⊙O是△ABC的內(nèi)切圓���,則點(diǎn)O是△ABC的( )
A.三條邊的垂直平分線的交點(diǎn)
B.三條角平分線的交點(diǎn)
C.三條中線的交點(diǎn)
D.三條高的交點(diǎn)
3.(2016·宜昌)在公園的O處附近有E����,F(xiàn)����,G,H四棵樹(shù)���,位置如圖所示(圖中小正方體的邊長(zhǎng)均相等)���,現(xiàn)計(jì)劃修建一座以O(shè)為圓心,OA為半徑的圓形水池���,要求池中不留樹(shù)木���,則E�����,F(xiàn)����,G��,H四棵樹(shù)中需要移除的是(
2���、 )
A.E��,F(xiàn)�,G B.F�,G,H
C.G���,H��,E D.H���,E,F(xiàn)
4.(2016·荊州)如圖,過(guò)⊙O外一點(diǎn)P引⊙O的兩條切線PA�,PB,切點(diǎn)分別是A�����,B��,OP交⊙O于點(diǎn)C����,點(diǎn)D是優(yōu)弧上不與點(diǎn)A��、點(diǎn)C重合的一個(gè)動(dòng)點(diǎn)���,連接AD����,CD.若∠APB=80°��,則∠ADC的度數(shù)是( )
A.15° B.20° C.25° D.30°
5.(2017·無(wú)錫)如圖�,菱形ABCD的邊AB=20,面積為320�,∠BAD<90°,⊙O與邊AB,AD都相切�����,AO=10�,則⊙O的半徑長(zhǎng)等于( )
A.5 B.6 C.2
3、 D.3
6.(2016·遵義)如圖�����,矩形ABCD中����,AB=4,BC=3��,連接AC����,⊙P和⊙Q分別是△ABC和△ADC的內(nèi)切圓,則PQ的長(zhǎng)是( )
A. B. C. D.2
7.如圖��,AB��,AC���,BD是⊙O的切線�����,P���,C���,D為切點(diǎn).如果AB=5,AC=3���,那么BD的長(zhǎng)為_(kāi)_____.
8.(2016·永州)如圖,給定一個(gè)半徑長(zhǎng)為2的圓�,圓心O到水平直線的距離為d,即OM=d.我們把圓上到直線l的距離等于1的點(diǎn)的個(gè)數(shù)記為m.如d=0時(shí)��,l為經(jīng)過(guò)圓心O的一條直線��,此時(shí)圓上有四個(gè)到直線l的距離等于1的點(diǎn)��,即m=4.由此可知:
(1)當(dāng)d=3時(shí)���,m=
4�����、________����;
(2)當(dāng)m=2時(shí),d的取值范圍是________.
9.如圖����,在矩形ABCD中,AB=4��,AD=3�,以頂點(diǎn)D為圓心作半徑為r的圓,若要求另外三個(gè)頂點(diǎn)A����,B,C中至少有一個(gè)點(diǎn)在圓內(nèi)�,且至少有一個(gè)點(diǎn)在圓外,則r的取值范圍是______________.
10.(2016·衢州)如圖��,AB為⊙O的直徑���,弦CD⊥AB����,垂足為點(diǎn)P,直線BF與AD的延長(zhǎng)線交于點(diǎn)F���,且∠AFB=∠ABC.
(1)求證:直線BF是⊙O的切線����;
(2)若CD=2����,OP=1,求線段BF的長(zhǎng).
11.(2017·武漢)已知一個(gè)三角形的三邊長(zhǎng)
5�、分別為5,7�����,8����,則其內(nèi)切圓的半徑為( )
A. B. C. D.2
12.如圖���,在矩形ABCD中����,AB=4,AD=5�,AD,AB����,BC分別與⊙O相切于E,F(xiàn)���,G三點(diǎn)���,過(guò)點(diǎn)D作⊙O的切線交BC于點(diǎn)M,切點(diǎn)為N���,則DM的長(zhǎng)為( )
A. B. C. D.2
13.(2016·攀枝花)如圖�����,△ABC中����,∠C=90°�,AC=3����,AB=5��,D為BC邊的中點(diǎn)�����,以AD上一點(diǎn)O為圓心的⊙O和AB�����,BC均相切�,則⊙O的半徑為_(kāi)_____.
14.(2017·湖州)如圖,已知∠AOB=30°���,在射線OA上取點(diǎn)O1���,以O(shè)1為圓心的圓與
6�、OB相切;在射線O1A上取點(diǎn)O2����,以O(shè)2為圓心���,O2O1為半徑的圓與OB相切;在射線O2A上取點(diǎn)O3����,以O(shè)3為圓心,O3O2為半徑的圓與OB相切�;…;在射線O9A上取點(diǎn)O10��,以O(shè)10為圓心�,O10O9為半徑的圓與OB相切.若⊙O1的半徑為1,則⊙O10的半徑長(zhǎng)是________.
15.(2017·常德)如圖����,已知AB是⊙O的直徑,CD與⊙O相切于C����,BE∥CO.
(1)求證:BC是∠ABE的平分線;
(2)若DC=8�����,⊙O的半徑OA=6,求CE的長(zhǎng).
16.(2017·陜西)如圖����,已知⊙O的半徑為5,PA是⊙O的一條切線��,切點(diǎn)為A�����,連接PO并延長(zhǎng)���,交⊙O
7��、于點(diǎn)B��,過(guò)點(diǎn)A作AC⊥PB交⊙O于點(diǎn)C����、交PB于點(diǎn)D�,連接BC,當(dāng)∠P=30°時(shí)��,
(1)求弦AC的長(zhǎng)����;
(2)求證:BC∥PA.
17.(2017·營(yíng)口)如圖,點(diǎn)E在以AB為直徑的⊙O上����,點(diǎn)C是的中點(diǎn),過(guò)點(diǎn)C作CD⊥AE�����,交AE的延長(zhǎng)線于點(diǎn)D�,連接BE交AC于點(diǎn)F.
(1)求證:CD是⊙O的切線;
(2)若cos∠CAD=����,BF=15,求AC的長(zhǎng).
要題加練8 與圓有關(guān)的角度計(jì)算
1.如圖��,AB是⊙O的直徑�,C,D兩點(diǎn)在⊙O上��,若∠C=45°����,求∠ABD的度數(shù).
2.如
8、圖,已知四邊形ABCD內(nèi)接于⊙O�,∠BOD=80°,求∠BCD的度數(shù).
3.如圖�,已知△ABC內(nèi)接于⊙O,CD是⊙O的切線與半徑OB的延長(zhǎng)線交于點(diǎn)D���,∠A=30°�,求∠BCD的度數(shù).
4.如圖���,已知AB是⊙O的直徑�,AC是⊙O的弦����,過(guò)點(diǎn)C的切線交AB的延長(zhǎng)線于點(diǎn)D,且∠A=∠D�,求∠D的度數(shù).
參考答案
【夯基過(guò)關(guān)】
1.A 2.B 3.A 4.C 5.C 6.B 7.2
8.(1)1 (2)1<d<3 9.3<r<5
10.(1)證明:∵∠
9、AFB=∠ABC����,∠ABC=∠ADC,
∴∠AFB=∠ADC���,∴CD∥BF.
∵CD⊥AB��,∴AB⊥BF���,∴直線BF是⊙O的切線.
(2)解:如圖�,連接OD���,
∵CD⊥AB,∴PD=CD=.
∵OP=1���,∴OD=2.
∵∠PAD=∠BAF�����,∠APD=∠ABF��,
∴△APD∽△ABF�,∴=��,即=�,
解得BF=.
【高分奪冠】
11.C 12.A
13. 14.29
15.(1)證明:∵DE是切線,∴OC⊥DE.
∵BE∥CO�,∴∠OCB=∠CBE.
∵OC=OB,∴∠OCB=∠OBC����,
∴∠CBE=∠OBC�,∴BC平分∠ABE.
(2)解:在Rt△CDO中�,
10、
∵DC=8�����,OC=OA=6�,
∴OD==10.
∵OC∥BE,
∴=����,
∴=,解得CE=4.8.
16.(1)解:如圖��,連接OA�,
∵PA是⊙O的切線,
∴∠PAO=90°.
∵∠P=30°��,∴∠AOD=60°.
∵AC⊥PB��,PB過(guò)圓心O���,∴AD=DC.
在Rt△ODA中�,AD=OA·sin 60°=,
∴AC=2AD=5.
(2)證明:∵AC⊥PB�,∠P=30°,
∴∠PAC=60°.
∵∠AOP=60°�����,∴∠BOA=120°����,
∴∠BCA=60°�����,∴∠PAC=∠BCA��,
∴BC∥PA.
17.(1)證明:如圖�,連接OC,
∵點(diǎn)C是的中點(diǎn)��,∴=�����,∴
11���、OC⊥BE.
∵AB是⊙O的直徑���,∴AD⊥BE�����,∴AD∥OC.
∵AD⊥CD���,∴OC⊥CD,
∴CD是⊙O的切線.
(2)解:如圖���,過(guò)點(diǎn)O作OM⊥AC于點(diǎn)M.
∵點(diǎn)C是的中點(diǎn)����,
∴=�,∠BAC=∠CAE,∴=.
∵cos∠CAD=��,∴=���,∴AB=BF=20.
在Rt△AOM中�����,∠AMO=90°���,AO=AB=10���,
cos∠OAM=cos∠CAD=,
∴AM=AO·cos∠OAM=8��,
∴AC=2AM=16.
要題加練8 與圓有關(guān)的角度計(jì)算
1.解:∵∠C=45°���,∴∠A=∠C=45°.
∵AB是⊙O的直徑�,∴∠ADB=90°�����,
∴∠ABD =45°.
2.解
12�、:∵∠BOD=80°�,∴∠BAD=40°.
又∵四邊形ABCD是圓的內(nèi)接四邊形,
∴∠BAD+∠BCD=180°���,
∴∠BCD=140°.
3.解:如圖�,連接OC.
∵CD是⊙O的切線�����,∴∠OCD=90°.
∵∠A=30°,∴∠COB=2∠A=60°.
∵OC=OB�����,∴△OBC是等邊三角形�,
∴∠OCB=60°,∴∠BCD=90°-∠OCB=30°.
4.解:如圖���,連接OC���,
∵CD是⊙O的切線,
∴OC⊥CD�,∴∠OCD=90°,
∴∠COB+∠D=90°.
由圓周角定理得∠COB=2∠A.
∵∠A=∠D�,∴2∠A+∠A=90°,
∴∠A=30°�����,∴∠D=30°.
9
 山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 第六章 圓 第二節(jié) 與圓有關(guān)的位置關(guān)系練習(xí)
山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 第六章 圓 第二節(jié) 與圓有關(guān)的位置關(guān)系練習(xí)