《2022秋九年級數(shù)學上冊 第1章 一元二次方程1.4 用一元二次方程解決問題 3用一元二次方程解幾何面積問題學案（新版）蘇科版》由會員分享，可在線閱讀，更多相關《2022秋九年級數(shù)學上冊 第1章 一元二次方程1.4 用一元二次方程解決問題 3用一元二次方程解幾何面積問題學案（新版）蘇科版（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、精品文檔
實際問題與一元二次方程(2)
學習目標：
〔1〕、掌握面積法建立一元二次方程的數(shù)學模型并運用它解決實際問題．
〔2〕、 利用提問的方法復習幾種特殊圖形的面積公式來引入新課，解決新課中的問題．
學習重點：據(jù)面積與面積之間的等量關系建立一元二元方程的數(shù)學模型并運用它解決實際問題．
學習難點：根據(jù)面積與面積之間的等量關系建立一元二次方程的數(shù)學模型．
〔一〕導學求思
1、列方程解應用題步驟
2、填空：1〕．直角三角形的面積公式是 一般
2、三角形的面積公式是
2〕．正方形的面積公式是 長方形的面積公式又是
3〕．梯形的面積公式是 4〕． 菱形的面積公式是
5〕．平行四邊形的面積公式是 6〕．圓的面積公式是
〔二〕、探究交流
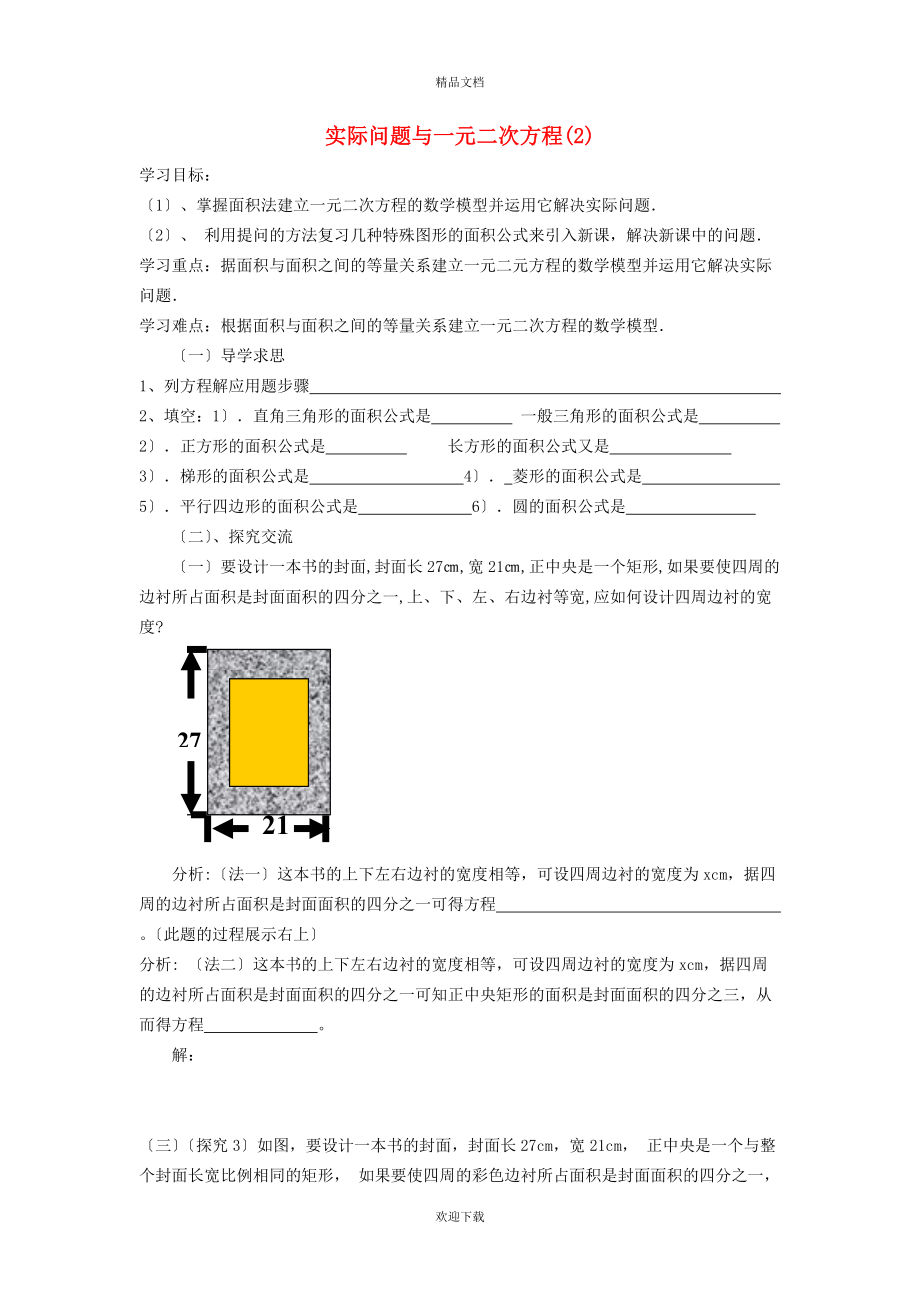
〔一〕要設計一本書的封面,封面長27㎝,寬21㎝,正中央是一個矩形,如果要使四周的邊襯所占面積是封面面積的四分之一,上、下、左、右邊襯等寬,應如何設計四周邊襯的寬度?
27
21
分析
3、:〔法一〕這本書的上下左右邊襯的寬度相等，可設四周邊襯的寬度為xcm，據(jù)四周的邊襯所占面積是封面面積的四分之一可得方程 ?！泊祟}的過程展示右上〕
分析: 〔法二〕這本書的上下左右邊襯的寬度相等，可設四周邊襯的寬度為xcm，據(jù)四周的邊襯所占面積是封面面積的四分之一可知正中央矩形的面積是封面面積的四分之三，從而得方程 。
解：
〔三〕〔探究3〕如圖，要設計一本書的封面，封面長27cm，寬21cm，正中央是一個與整個封面長寬比例相同的矩形，如果要使四周的彩色邊襯所占面積是封面面積的四分
4、之一，上、下邊襯等寬，左、右邊襯等寬，應如何設計四周邊襯的寬度〔結果保存小數(shù)點后一位〕？
27
21
分析:〔法一〕這本書的長寬之比是9:7,依題知正中央的矩形兩邊之比也為9:7，設正中央的矩形兩邊分別為9xcm，7xcm，那么上、下邊襯為 ，左、右邊襯為 因為四周的彩色邊襯所點面積是封面面積的四分之一，那么中央矩形的面積是封面面積的四分之三，從而得方程 ?；蛑苯痈鶕?jù)四周的彩色邊襯所點面積是封面面積的四分之一得方程 ?！泊祟}展示于右上〕
分析:〔法二〕
依據(jù)題意知：中央矩形的長寬之比等于封面的長寬之比＝9：7，由此可以判定：上下邊襯寬與左右邊襯寬之比為9：7，設上、下邊襯的寬均為9xcm，那么左、右邊襯的寬均為7xcm，依題意，得：中央矩形的長為〔 〕cm，寬為〔 〕cm． 因為四周的彩色邊襯所點面積是封面面積的四分之一，那么中央矩形的面積是封面面積的四分之三．從而得方程 ?；蛑苯痈鶕?jù)四周的彩色邊襯所點面積是封面面積的四分之一得方程 。
解：
歡迎下載
2022秋九年級數(shù)學上冊 第1章 一元二次方程1.4 用一元二次方程解決問題 3用一元二次方程解幾何面積問題學案（新版）蘇科版
