《高中數(shù)學 第二章 函數(shù)概念與基本初等函數(shù)I 2.1 函數(shù)的概念 2.1.1 函數(shù)的概念和圖象2時學案 蘇教版必修1》由會員分享����,可在線閱讀����,更多相關《高中數(shù)學 第二章 函數(shù)概念與基本初等函數(shù)I 2.1 函數(shù)的概念 2.1.1 函數(shù)的概念和圖象2時學案 蘇教版必修1(6頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、
2.1.1 函數(shù)的概念
第2課時 函數(shù)的圖象
在實際情境中了解圖象法是描述兩個變量之間函數(shù)關系的一種重要方法.通過函數(shù)圖象��,從“形”的角度進一步加深對函數(shù)概念的理解.
函數(shù)的圖象
將自變量的一個值x0作為橫坐標��,相應的函數(shù)值f(x0)作為縱坐標�����,就得到坐標平面上的一個點(x0��,f(x0)).當自變量取遍函數(shù)定義域A中的每一個值時���,就得到一系列這樣的點.所有這些點組成的集合(點集)為{(x,f(x))|x∈A}����,即{(x,y)|y=f(x)���,x∈A}���,所有這些點組成的圖形就是函數(shù)y=f(x)的圖象.
作函數(shù)圖象�,應明確函數(shù)定義域�,明確函數(shù)圖象形狀,體會定義域?qū)D象的控制
2��、作用.
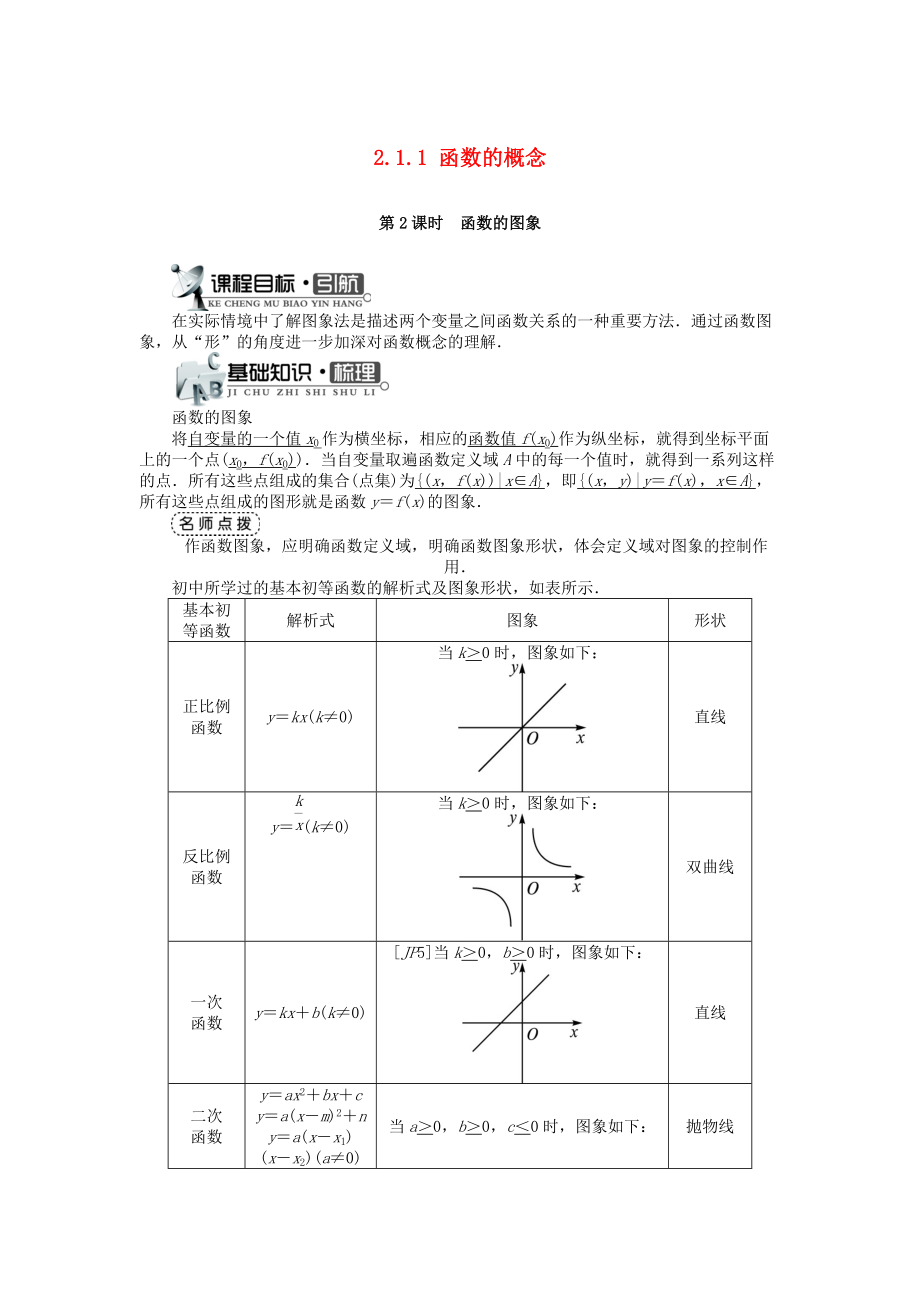
初中所學過的基本初等函數(shù)的解析式及圖象形狀�,如表所示.
基本初等函數(shù)
解析式
圖象
形狀
正比例
函數(shù)
y=kx(k≠0)
當k>0時,圖象如下:
直線
反比例
函數(shù)
y=(k≠0)
當k>0時��,圖象如下:
雙曲線
一次
函數(shù)
y=kx+b(k≠0)
[JP5]當k>0��,b>0時�����,圖象如下:
直線
二次
函數(shù)
y=ax2+bx+c
y=a(x-m)2+n
y=a(x-x1)(x-x2)(a≠0)
當a>0�����,b>0��,c<0時����,圖象如下:
拋物線
函數(shù)新概念���,記準要素三;定義域值域��,關系式相連��;函數(shù)表示法�����,記住也不
3、難��;圖象和列表�����,解析最常見.
【做一做1-1】作出函數(shù)y=x2-2x在[0,3]上的圖象.
解:圖象如下:
【做一做1-2】在同一直角坐標系中����,分別作出直線y1=x-2和雙曲線y2=的圖象,并根據(jù)圖象回答x取何值時�����,(1)y1>y2;(2)y1=y(tǒng)2�����;(3)y1<y2.
解:圖象如圖所示.
(1)當x∈(-1,0)∪(3���,+∞)時���,y1>y2;
(2)當x=-1或3時��,y1=y(tǒng)2��;
(3)當x∈(-∞����,-1)∪(0,3)時,y1<y2.
函數(shù)的圖象都是連續(xù)的曲線嗎�����?圖形都是函數(shù)的圖象嗎���?
剖析:(1)函數(shù)的圖象不一定都是連續(xù)的曲線.一般來說����,如果自變量的取值是連續(xù)
4��、的��,那么它的圖象是連續(xù)的��,如一次函數(shù)����、二次函數(shù)��,但如果自變量的取值不是連續(xù)的���,那么它的圖象就是一些孤立點.例如:y=3x(x∈{1,2,3,4,5}).有時函數(shù)的圖象是由幾段線段組成.
(2)檢查一個圖形是否為某個函數(shù)的圖象,只要用一條垂直于x軸的直線沿x軸方向左右平移�����,觀察圖形與該直線交點個數(shù),當交點個數(shù)為兩個或兩個以上時�����,該圖形一定不是函數(shù)圖象.這是因為直線x=a(a∈R)與圖形有兩個或兩個以上交點時��,表示變量x取實數(shù)a時對應兩個或兩個以上的y值�,這與只有惟一y值與x對應矛盾.
題型一 函數(shù)的圖象
【例1】設M={x|0≤x≤2}�,N={y|0≤y≤2},下面的四個圖形中能表示
5�����、從集合M到集合N的函數(shù)關系的是__________.
解析:由函數(shù)的定義知①不是����,因為集合M中1<x≤2時,在N中無元素與之對應���;③中x=2對應的元素y=3N,所以③不是����;④中x=1時,在N中有兩個元素與之對應,④也不是.
答案:②
【例2】試畫出下列函數(shù)的圖象:
(1)f(x)=2x-1�����;
(2)f(x)=(x+1)2-1�����,x∈(-3,0].
解:描點����,作出圖象�����,則函數(shù)圖象分別如下圖(1)(2)所示.
(1) (2)
反思:當自變量x的定義域為某一區(qū)間時��,其函數(shù)y=f(x)的圖象也是某一局部��,本題(2)中��,(-3,3)是空心點���,(0,0)是實心點
6、.
題型二 圖象的應用
【例3】求下列函數(shù)的值域:
(1)y=-x2-2x+3(-5≤x≤-2);
(2)y=x+.
解:(1)可以用“圖象法”���,根據(jù)自變量的變化范圍(-5≤x≤-2)來確定y=-x2-2x+3的值的變化范圍.
∵y=-x2-2x+3=-(x+1)2+4,其圖象是開口向下的拋物線�����,頂點坐標為(-1,4)�����,
當x∈[-5�,-2]時��,其圖象如圖所示.
∴當x=-5時��,ymin=-12�����;
當x=-2時��,ymax=3.
∴y=-x2-2x+3(-5≤x≤-2)的值域是[-12,3].
(2)可以通過“變量代換法”把問題轉(zhuǎn)化成二次函數(shù)�,再求其值域.要注意在
7�����、進行換元的過程中��,新變量的取值范圍.設�����,則u≥0���,且,
∴.
其圖象如圖所示�,由圖象可知.
∴函數(shù)的值域為.
反思:本題介紹了兩種求函數(shù)值域的方法:①圖象法:通過圖象觀察知函數(shù)在某一定義域內(nèi)的最值;②換元法:通過換元���,將某些函數(shù)化歸為我們熟知的函數(shù)�,再求值域.
【例4】如圖����,已知拋物線與x軸交于A(-1,0)����、E(3,0)兩點����,與y軸交于點B(0,3).
(1)求拋物線的解析式��;
(2)分別寫出當x取何值時����,y<0�����,y=0����,y>0;
(3)設拋物線頂點為D�,求四邊形AEDB的面積.
分析:根據(jù)待定系數(shù)法,求出二次函數(shù)的解析式�,再從圖象上觀察,位于x軸上方部分的點����,其縱坐標
8、y>0��;下方部分的點,其縱坐標y<0.
解:(1)設y=ax2+bx+c�,
則由條件得
解之,得從而y=-x2+2x+3.
(2)令y=0,得-x2+2x+3=0,x1=-1���,x2=3���,
所以當x>3或x<-1時��,y<0�����;
當x=3或x=-1時����,y=0�;
當-1<x<3時,y>0.
(3)因為y=-(x-1)2+4�,
所以點D(1,4).
從而S四邊形AEDB=×3×1+×(3+4)×1+×4×2=9.
反思:我們可以利用函數(shù)圖象來求解形如ax2+bx+c>0和ax2+bx+c<0(a≠0)的不等式.
1二
9、次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示�����,有下列4個結(jié)論:①abc>0;②b<a+c���;③4a+2b+c>0�;④b2-4ac>0.其中正確的結(jié)論有__________個.
解析:圖象開口向下�����,所以a<0.
圖象與y軸交于正半軸�,所以c>0.
因為-=1��,
所以b=-2a>0.
從而abc<0���,結(jié)論①錯誤��;
當x=-1時����,y=a-b+c<0���,得b>a+c�����,結(jié)論②錯誤����;
由對稱性可知,當x=2時��,4a+2b+c>0��,
所以結(jié)論③正確���;
又因為拋物線與x軸有兩個交點�����,
所以Δ=b2-4ac>0.所以結(jié)論④正確.
答案:2
2下列各圖�����,可以作為以x為自變量的函數(shù)的圖
10��、象的有________.
答案:②④
3已知拋物線y=ax2+bx+c(a>0)的對稱軸為直線x=1�,且經(jīng)過點(-1��,y1),(2��,y2)�����,試比較y1和y2的大?��。簓1__________y2(填“>”“<”或“=”).
解析:因為對稱軸為x=1���,
所以當x=2時與x=0時的函數(shù)值相等.
作出如圖所示的大致圖象�,由圖象可知,y1>y2.
答案:>
求函數(shù)y=(x∈[4,5])的值域.
解:f(x)==�,
∵x∈[4,5],∴(x-1)2+1∈[10,17].
∴∈.
即所求函數(shù)的值域為.
6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375
 高中數(shù)學 第二章 函數(shù)概念與基本初等函數(shù)I 2.1 函數(shù)的概念 2.1.1 函數(shù)的概念和圖象2時學案 蘇教版必修1
高中數(shù)學 第二章 函數(shù)概念與基本初等函數(shù)I 2.1 函數(shù)的概念 2.1.1 函數(shù)的概念和圖象2時學案 蘇教版必修1