《高考數(shù)學(xué)二輪專題復(fù)習(xí)與策略 第1部分 專題4 立體幾何 突破點10 空間幾何體表面積或體積的求解專題限時集訓(xùn) 理-人教版高三數(shù)學(xué)試題》由會員分享����,可在線閱讀,更多相關(guān)《高考數(shù)學(xué)二輪專題復(fù)習(xí)與策略 第1部分 專題4 立體幾何 突破點10 空間幾何體表面積或體積的求解專題限時集訓(xùn) 理-人教版高三數(shù)學(xué)試題(11頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1��、專題限時集訓(xùn)(十) 空間幾何體表面積或體積的求解
[建議A�����、B組各用時:45分鐘]
[A組 高考達(dá)標(biāo)]
一�、選擇題
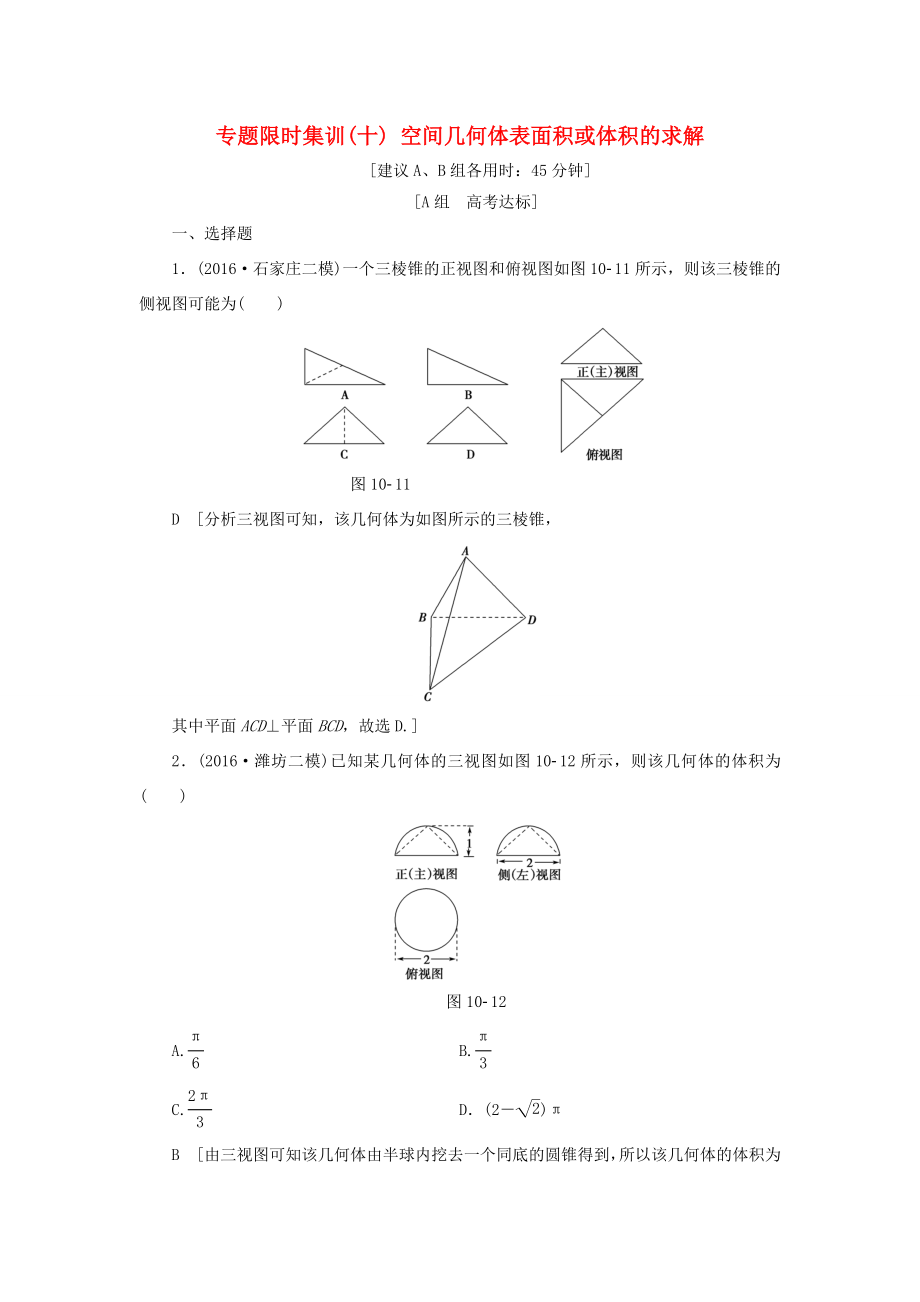
1.(2016·石家莊二模)一個三棱錐的正視圖和俯視圖如圖10-11所示��,則該三棱錐的側(cè)視圖可能為( )
圖10-11
D [分析三視圖可知��,該幾何體為如圖所示的三棱錐��,
其中平面ACD⊥平面BCD�����,故選D.]
2.(2016·濰坊二模)已知某幾何體的三視圖如圖10-12所示,則該幾何體的體積為( )
圖10-12
A. B.
C. D.(2-)π
B [由三視圖可知該幾何體由半球內(nèi)挖去一個同底的
2�、圓錐得到,所以該幾何體的體積為V=×π×13-π×12×1=.]
3.(2016·煙臺模擬)某幾何體的三視圖如圖10-13所示���,則該幾何體的體積與其外接球的體積之比為( )
圖10-13
A.1∶3π B.∶π
C.1∶3π D.1∶π
D [由三視圖可知�����,幾何體是一個三棱柱�����,體積V1=×2×2×2=4����,設(shè)外接球的半徑為R�,則4R2=22+22+22=12,所以R=.
所以球的體積V2=πR3=4π����,體積比V1∶V2=4∶4π=1∶π.]
4.(2016·湖北七市模擬)已知某幾何體的三視圖如圖10-14所示,其中俯視圖是正三角形���,則該幾何體的體積為( )
圖10-1
3�����、4
A. B.2
C.3 D.4
B [分析題意可知���,該幾何體是由如圖所示的三棱柱ABC-A1B1C1截去四棱錐A-BEDC得到的��,故其體積V=×22×3-××2×=2�����,故選B.]
5.(2016·廣州二模)如圖10-15����,網(wǎng)格紙上小正方形的邊長為1���,粗線畫出的是某個四面體的三視圖,則該四面體的表面積為( )
圖10-15
A.8+8+4 B.8+8+2
C.2+2+ D.++
A [在正方體中還原出該四面體C-A1EC1如圖所示��,可求得該四面體的表面積為8+8+4.]
二�、填空題
6.(2016·昆明一模)已知三棱錐P-ABC的頂點P,A�����,B,C在球
4�、O的球面上,△ABC是邊長為的等邊三角形����,如果球O的表面積為36π,那么P到平面ABC距離的最大值為________.
3+2 [依題意��,邊長是的等邊△ABC的外接圓半徑r=·=1.∵球O的表面積為36π=4πR2�����,∴球O的半徑R=3��,∴球心O到平面ABC的距離d==2��,∴球面上的點P到平面ABC距離的最大值為R+d=3+2.]
7.(2016·山東省實驗中學(xué)模擬)三棱錐P-ABC中����,D,E分別為PB�����,PC的中點�����,記三棱錐D-ABE的體積為V1,P-ABC的體積為V2���,則=________.
[如圖����,設(shè)S△ABD=S1�����,S△PAB=S2���,
E到平面ABD的距離為h1�����,C到平面PA
5、B的距離為h2�,則S2=2S1,h2=2h1���,V1=S1h1��,V2=S2h2�����,所以==.]
8.(2016·?��?诙?半徑為2的球O中有一內(nèi)接正四棱柱(底面是正方形����,側(cè)棱垂直底面).當(dāng)該正四棱柱的側(cè)面積最大時���,球的表面積與該正四棱柱的側(cè)面積之差是________.
16(π-) [設(shè)內(nèi)接正四棱柱底邊長為a���,高為h,那么16=2a2+h2≥2ah�����,正四棱柱的側(cè)面積S=4ah≤16�����,球的表面積與該正四棱柱的側(cè)面積之差是16(π-).]
三�����、解答題
9.(2016·合肥二模)如圖10-16,P為正方形ABCD外一點�����,PB⊥平面ABCD�,PB=AB=2,E為PD的中點.
圖10-16
6�����、(1)求證:PA⊥CE�����;
(2)求四棱錐P-ABCD的表面積.
[解] (1)證明:取PA的中點F��,連接EF�����,BF����,則EF∥AD∥BC,即EF����,BC共面.
∵PB⊥平面ABCD,∴PB⊥BC�,又BC⊥AB且PB∩AB=B,
∴BC⊥平面PAB�,∴BC⊥PA.3分
∵PB=AB,∴BF⊥PA����,又BC∩BF=B,
∴PA⊥平面EFBC���,∴PA⊥CE.6分
(2)設(shè)四棱錐P-ABCD的表面積為S����,
∵PB⊥平面ABCD���,∴PB⊥CD��,又CD⊥BC�����,PB∩BC=B���,
∴CD⊥平面PBC�����,∴CD⊥PC����,即△PCD為直角三角形�,8分
由(1)知BC⊥平面PAB,而AD∥BC�,∴AD⊥平
7、面PAB����,
故AD⊥PA,即△PAD也為直角三角形.
S?ABCD=2×2=4�����,
S△PBC=S△PAB=S△PDA=×2×2=2�����,
S△PCD=×2×=2�����,10分
∴S表=S?ABCD+S△PBC+S△PDA+S△PAB+S△PCD
=10+2.12分
10.(2016·湖北七市模擬)如圖10-17����,一個側(cè)棱長為l的直三棱柱ABC-A1B1C1容器中盛有液體(不計容器厚度).若液面恰好分別過棱AC,BC����,B1C1,A1C1的中點D�,E,F(xiàn)��,G.
圖10-17
(1)求證:平面DEFG∥平面ABB1A1���;
(2)當(dāng)?shù)酌鍭BC水平放置時��,求液面的高.
[解] (1)證明
8���、:因為D,E分別為棱AC,BC的中點�����,所以DE是△ABC的中位線����,所以DE∥AB.又DE?平面ABB1A1,AB?平面ABB1A1�,所以DE∥平面ABB1A1.同理DG∥平面ABB1A1,又DE∩DG=D��,所以平面DEFG∥平面ABB1A1.6分
(2)當(dāng)直三棱柱ABC-A1B1C1容器的側(cè)面AA1B1B水平放置時���,由(1)可知����,液體部分是直四棱柱���,其高即為原直三棱柱ABC-A1B1C1容器的高���,即側(cè)棱長l,當(dāng)?shù)酌鍭BC水平放置時�����,設(shè)液面的高為h,△ABC的面積為S���,則由已知條件可知,△CDE∽△ABC���,且S△CDE=S��,所以S四邊形ABED=S.9分
由于兩種狀態(tài)下液體體積相等��,所以V液
9�、體=Sh=S四邊形ABEDl=Sl�����,即h=l.
因此�����,當(dāng)?shù)酌鍭BC水平放置時��,液面的高為l.12分
[B組 名校沖刺]
一���、選擇題
1.(2016·濟(jì)寧模擬)如圖10-18所示�����,四棱錐P-ABCD中���,PD⊥平面ABCD�,且PD=2��,底面是邊長為2的菱形���,M是CD的中點�,平面PMB⊥平面PCD�,則該四棱錐的體積為( )
圖10-18
A. B.4
C. D.4
A [過點D在平面PCD內(nèi)作DN⊥PM于點N,又平面PMB⊥平面PCD���,平面PMB∩平面PCD=PM�����,所以DN⊥平面PMB����,所以DN⊥BM.又由PD⊥平面ABCD,得PD⊥BM�����,又PD與DN是平面PDC內(nèi)的兩條相交直
10���、線�����,所以BM⊥平面PDC,則BM⊥CD.又點M是CD的中點�����,BC=CD�,所以∠BCD=60°,所以底面菱形ABCD的面積為2×2×sin 60°=2���,故該四棱錐的體積為×2×2=.]
2.(2016·重慶二模)某幾何體的三視圖如圖10-19所示��,則該幾何體的體積為( )
圖10-19
A. B.
C. D.
B [根據(jù)三視圖可知���,幾何體是由一個直三棱柱與一個三棱錐所組成的��,其中該直三棱柱的底面是一個直角三角形(直角邊長分別為1,2���,高為1);該三棱錐的底面是一個直角三角形(腰長分別為1,2��,高為1)���,因此該幾何體的體積為×2×1×1+××2×1×1=����,選B.]
3.(2016
11�����、·唐山二模)某幾何體的三視圖如圖10-20所示�����,則該幾何體的體積為( )
圖10-20
A.6π+4 B.π+4
C. D.2π
D [由三視圖知����,該幾何體為一個底面半徑為1,高為1的圓柱體��,與底面半徑為1,高為2的半圓柱體構(gòu)成��,所以該三視圖的體積為π×12×1+π×12×2=2π����,故選D.]
4.(2016·江西上饒三模)從點P出發(fā)的三條射線PA,PB���,PC兩兩成60°角����,且分別與球O相切于A����,B��,C三點��,若OP=����,則球的體積為( )
A. B.
C. D.
C [設(shè)OP交平面ABC于O′,
由題得△ABC和△PAB為正三角形�����,
所以O(shè)′A=AB=AP.
因為A
12、O′⊥PO�����,OA⊥PA�,
所以=,=�,=,
所以O(shè)A==×=1�,
即球的半徑為1,
所以其體積為π×13=π.選C.]
二��、填空題
5.(2016·廣州二模)一個六棱柱的底面是正六邊形���,側(cè)棱垂直于底面��,所有棱的長都為1����,頂點在同一個球面上�,則該球的體積為________.
【導(dǎo)學(xué)號:67722038】
[由題意知六棱柱的底面正六邊形的外接圓半徑r=1, 其高h(yuǎn)=1,∴球半徑為R===,∴該球的體積V=πR3=×3π=.]
6.(2016·開封一模)在三棱錐P-ABC中�����,AB=BC=�����,AC=6�����,PC⊥平面ABC�����,PC=2���,則該三棱錐的外接球表面積為________. 【導(dǎo)學(xué)
13��、號:67722039】
π [由題可知,△ABC中AC邊上的高為=����,球心O在底面ABC的投影即為△ABC的外心D,設(shè)DA=DB=DC=x�����,∴x2=32+(-x)2,解得x=�����,∴R2=x2+2=+1=(其中R為三棱錐外接球的半徑)�,∴外接球的表面積S=4πR2=π.]
三、解答題
7.如圖10-21��,矩形CDEF和梯形ABCD互相垂直����,∠BAD=∠ADC=90°,AB=AD=CD�,BE⊥DF.
圖10-21
(1)若M為EA中點,求證:AC∥平面MDF���;
(2)若AB=2����,求四棱錐E-ABCD的體積.
[解] (1)證明:設(shè)EC與DF交于點N�,連接MN,
在矩形CDEF中,點
14��、N為EC中點�����,
因為M為EA中點�����,所以MN∥AC.2分
又因為AC?平面MDF�,MN?平面MDF,
所以AC∥平面MDF.4分
(2)取CD中點為G���,連接BG�����,EG�����,
平面CDEF⊥平面ABCD��,平面CDEF∩平面ABCD=CD,
AD?平面ABCD,AD⊥CD�����,
所以AD⊥平面CDEF���,同理ED⊥平面ABCD����,7分
所以ED的長即為四棱錐E-ABCD的高.8分
在梯形ABCD中��,AB=CD=DG���,AB∥DG���,
所以四邊形ABGD是平行四邊形,BG∥AD���,所以BG⊥平面CDEF.
又DF?平面CDEF���,所以BG⊥DF,又BE⊥DF���,BE∩BG=B���,
所以DF⊥平面BEG
15���、,DF⊥EG.10分
注意到Rt△DEG∽Rt△EFD���,所以DE2=DG·EF=8���,DE=2,
所以VE-ABCD=S梯形ABCD·ED=4.12分
8.如圖10-22���,在多面體ABCDM中���,△BCD是等邊三角形,△CMD是等腰直角三角形���,∠CMD=90°���,平面CMD⊥平面BCD,AB⊥平面BCD���,點O為CD的中點���,連接OM.
圖10-22
(1)求證:OM∥平面ABD;
(2)若AB=BC=2���,求三棱錐A-BDM的體積.
[解] (1)證明:∵△CMD是等腰直角三角形���,∠CMD=90°,點O為CD的中點���,∴OM⊥CD.1分
∵平面CMD⊥平面BCD���,平面CMD∩平面BCD
16、=CD���,OM?平面CMD���,
∴OM⊥平面BCD.2分
∵AB⊥平面BCD,∴OM∥AB.3分
∵AB?平面ABD���,OM?平面ABD���,∴OM∥平面ABD.4分
(2)法一:由(1)知OM∥平面ABD���,
∴點M到平面ABD的距離等于點O到平面ABD的距離.5分
過點O作OH⊥BD,垂足為點H.
∵AB⊥平面BCD���,OH?平面BCD���,∴OH⊥AB.6分
∵AB?平面ABD,BD?平面ABD���,AB∩BD=B���,∴OH⊥平面ABD.7分
∵AB=BC=2,△BCD是等邊三角形���,
∴BD=2���,OD=1,OH=OD·sin 60°=.9分
∴V三棱錐A-BDM=V三棱錐M-ABD
=××AB·BD·OH
=××2×2×=.11分
∴三棱錐A-BDM的體積為.12分
法二:由(1)知OM∥平面ABD���,
∴點M到平面ABD的距離等于點O到平面ABD的距離.5分
∵AB=BC=2���,△BCD是等邊三角形���,∴BD=2,OD=1.6分
連接OB���,則OB⊥CD,OB=BD·sin 60°=.7分
∴V三棱錐A-BDM=V三棱錐M-ABD=V三棱錐O-ABD=V三棱錐A-BDO
=××OD·OB·AB
=××1××2=.11分
∴三棱錐A-BDM的體積為.12分
 高考數(shù)學(xué)二輪專題復(fù)習(xí)與策略 第1部分 專題4 立體幾何 突破點10 空間幾何體表面積或體積的求解專題限時集訓(xùn) 理-人教版高三數(shù)學(xué)試題
高考數(shù)學(xué)二輪專題復(fù)習(xí)與策略 第1部分 專題4 立體幾何 突破點10 空間幾何體表面積或體積的求解專題限時集訓(xùn) 理-人教版高三數(shù)學(xué)試題