《2013年高中數(shù)學(xué) 暑期特獻(xiàn) 重要知識(shí)點(diǎn) 常量與變量》由會(huì)員分享，可在線閱讀，更多相關(guān)《2013年高中數(shù)學(xué) 暑期特獻(xiàn) 重要知識(shí)點(diǎn) 常量與變量（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、常量與變量
⑴、變量的定義：我們?cè)谟^察某一現(xiàn)象的過(guò)程時(shí)，常常會(huì)遇到各種不同的量，其中有的量在過(guò)程中不起變化，我們把其稱之為常量；有的量在過(guò)程中是變化的，也就是可以取不同的數(shù)值，我們則把其稱之為變量。注：在過(guò)程中還有一種量，它雖然是變化的，但是它的變化相對(duì)于所研究的對(duì)象是極其微小的，我們則把它看作常量。
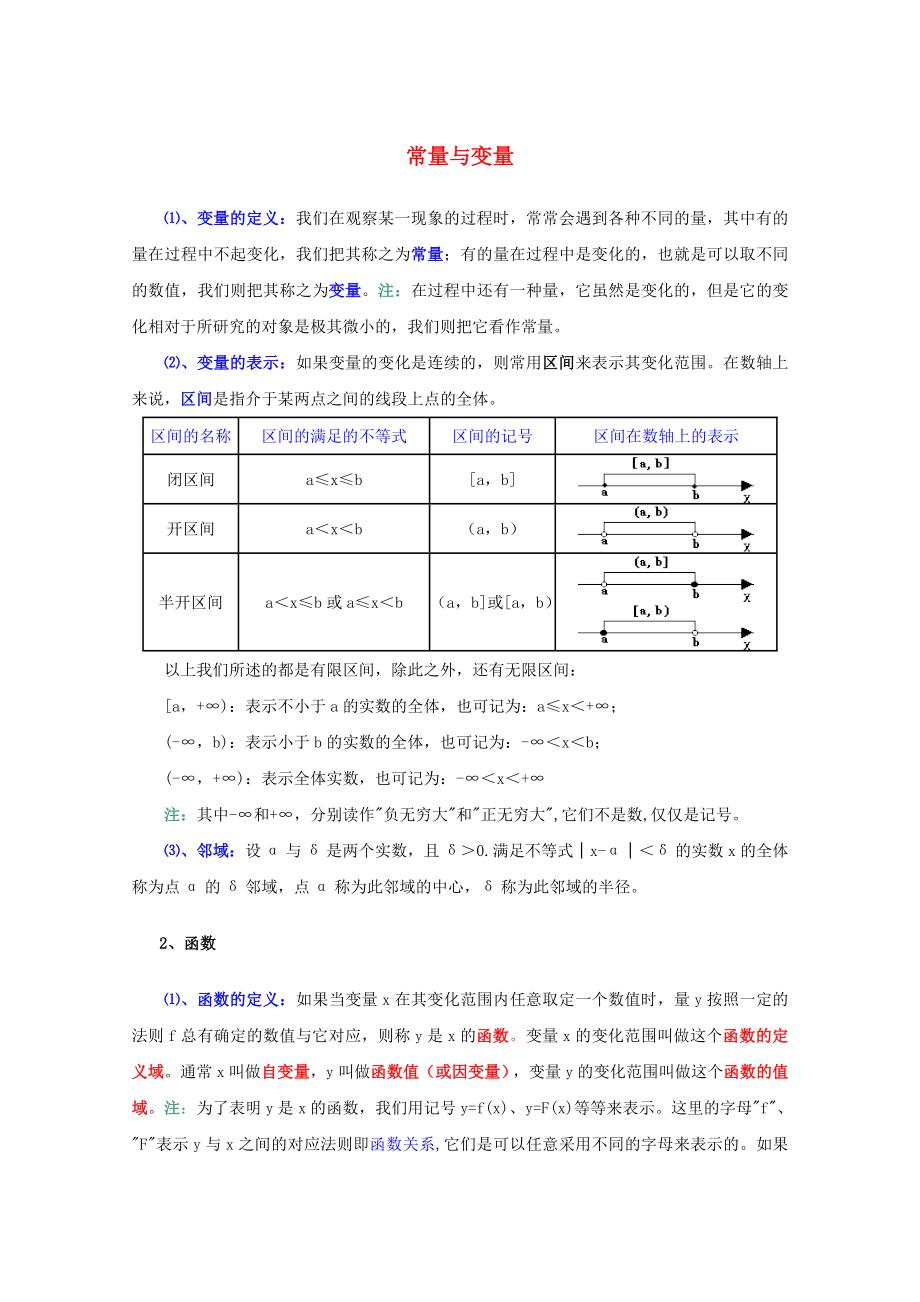
⑵、變量的表示：如果變量的變化是連續(xù)的，則常用區(qū)間來(lái)表示其變化范圍。在數(shù)軸上來(lái)說(shuō)，區(qū)間是指介于某兩點(diǎn)之間的線段上點(diǎn)的全體。
區(qū)間的名稱
區(qū)間的滿足的不等式
區(qū)間的記號(hào)
區(qū)間在數(shù)軸上的表示
閉區(qū)間
a≤x≤b
[a，b]
開(kāi)區(qū)間
a＜x＜b
（a，b）
半開(kāi)區(qū)間
2、
a＜x≤b或a≤x＜b
（a，b]或[a，b）
以上我們所述的都是有限區(qū)間，除此之外，還有無(wú)限區(qū)間：
[a，+∞)：表示不小于a的實(shí)數(shù)的全體，也可記為：a≤x＜+∞；
(-∞，b)：表示小于b的實(shí)數(shù)的全體，也可記為：-∞＜x＜b；
(-∞，+∞)：表示全體實(shí)數(shù)，也可記為：-∞＜x＜+∞
注：其中-∞和+∞，分別讀作"負(fù)無(wú)窮大"和"正無(wú)窮大",它們不是數(shù),僅僅是記號(hào)。
⑶、鄰域：設(shè)α與δ是兩個(gè)實(shí)數(shù)，且δ＞0.滿足不等式│x-α│＜δ的實(shí)數(shù)x的全體稱為點(diǎn)α的δ鄰域，點(diǎn)α稱為此鄰域的中心，δ稱為此鄰域的半徑。
2、函數(shù)
⑴、函數(shù)的定義：如果當(dāng)變量x在其變化范圍內(nèi)任意取定一
3、個(gè)數(shù)值時(shí)，量y按照一定的法則f總有確定的數(shù)值與它對(duì)應(yīng)，則稱y是x的函數(shù)。變量x的變化范圍叫做這個(gè)函數(shù)的定義域。通常x叫做自變量，y叫做函數(shù)值（或因變量），變量y的變化范圍叫做這個(gè)函數(shù)的值域。注：為了表明y是x的函數(shù)，我們用記號(hào)y=f(x)、y=F(x)等等來(lái)表示。這里的字母"f"、"F"表示y與x之間的對(duì)應(yīng)法則即函數(shù)關(guān)系,它們是可以任意采用不同的字母來(lái)表示的。如果自變量在定義域內(nèi)任取一個(gè)確定的值時(shí)，函數(shù)只有一個(gè)確定的值和它對(duì)應(yīng)，這種函數(shù)叫做單值函數(shù)，否則叫做多值函數(shù)。這里我們只討論單值函數(shù)。
⑵、函數(shù)相等
由函數(shù)的定義可知，一個(gè)函數(shù)的構(gòu)成要素為：定義域、對(duì)應(yīng)關(guān)系和值域。由于值域是由定義域和對(duì)應(yīng)關(guān)系決定的，所以，如果兩個(gè)函數(shù)的定義域和對(duì)應(yīng)關(guān)系完全一致，我們就稱兩個(gè)函數(shù)相等。
⑶、域函數(shù)的表示方法
a)：解析法：用數(shù)學(xué)式子表示自變量和因變量之間的對(duì)應(yīng)關(guān)系的方法即是解析法。例：直角坐標(biāo)系中，半徑為r、圓心在原點(diǎn)的圓的方程是：x2+y2=r2
b)：表格法：將一系列的自變量值與對(duì)應(yīng)的函數(shù)值列成表來(lái)表示函數(shù)關(guān)系的方法即是表格法。例：在實(shí)際應(yīng)用中，我們經(jīng)常會(huì)用到的平方表，三角函數(shù)表等都是用表格法表示的函數(shù)。
c)：圖示法：用坐標(biāo)平面上曲線來(lái)表示函數(shù)的方法即是圖示法。一般用橫坐標(biāo)表示自變量，縱坐標(biāo)表示因變量。例：直角坐標(biāo)系中，半徑為r、圓心在原點(diǎn)的圓用圖示法表示為：
2013年高中數(shù)學(xué) 暑期特獻(xiàn) 重要知識(shí)點(diǎn) 常量與變量
