《（人教通用）2022年中考數(shù)學(xué)總復(fù)習(xí) 第六章 圓 第23課時 尺規(guī)作圖知能優(yōu)化訓(xùn)練》由會員分享，可在線閱讀，更多相關(guān)《（人教通用）2022年中考數(shù)學(xué)總復(fù)習(xí) 第六章 圓 第23課時 尺規(guī)作圖知能優(yōu)化訓(xùn)練（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、（人教通用）2022年中考數(shù)學(xué)總復(fù)習(xí) 第六章 圓 第23課時 尺規(guī)作圖知能優(yōu)化訓(xùn)練
中考回顧
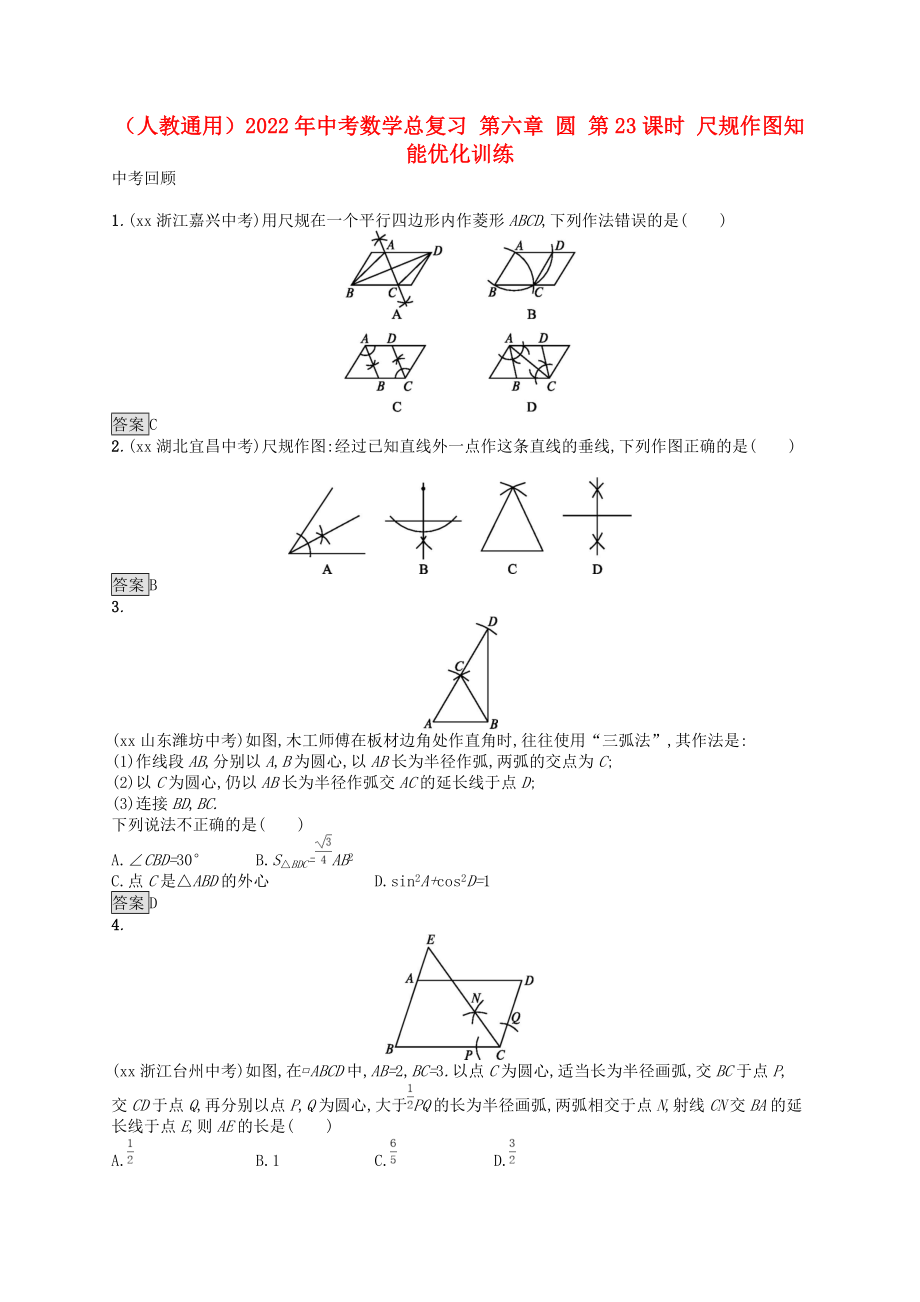
1.(xx浙江嘉興中考)用尺規(guī)在一個平行四邊形內(nèi)作菱形ABCD,下列作法錯誤的是( )
答案C
2.(xx湖北宜昌中考)尺規(guī)作圖:經(jīng)過已知直線外一點作這條直線的垂線,下列作圖正確的是( )
答案B
3.
(xx山東濰坊中考)如圖,木工師傅在板材邊角處作直角時,往往使用“三弧法”,其作法是:
(1)作線段AB,分別以A,B為圓心,以AB長為半徑作弧,兩弧的交點為C;
(2)以C為圓心,仍以AB長為半徑作弧交AC的延長線于點D;
2、(3)連接BD,BC.
下列說法不正確的是( )
A.∠CBD=30° B.S△BDC=AB2
C.點C是△ABD的外心 D.sin2A+cos2D=1
答案D
4.
(xx浙江臺州中考)如圖,在?ABCD中,AB=2,BC=3.以點C為圓心,適當(dāng)長為半徑畫弧,交BC于點P,交CD于點Q,再分別以點P,Q為圓心,大于PQ的長為半徑畫弧,兩弧相交于點N,射線CN交BA的延長線于點E,則AE的長是( )
A. B.1 C. D.
答案B
模擬預(yù)測
1.如圖,C,D分別是線段AB,AC的中點,分別以點C,D為圓心,BC長為半徑畫弧,兩弧交于點M,測量∠AMB的度數(shù),結(jié)
3、果為( )
A.80° B.90° C.100° D.105°
答案B
2.如圖,已知△ABC,AB
4、答案A
4.
如圖,已知線段a,h,求作等腰三角形ABC,使AB=AC,且BC=a,BC邊上的高AD=h.
張紅的作法是:
(1)作線段BC=a;
(2)作線段BC的垂直平分線MN,MN與BC相交于點D;
(3)在直線MN上截取線段h,確定點A;
(4)連接AB,AC,△ABC即為所求作的等腰三角形.
上述作法的四個步驟中,你認為有錯誤的一步是( )
A.(1) B.(2) C.(3) D.(4)
答案C
5.
如圖,點C在∠AOB的OB邊上,用尺規(guī)作出了CN∥OA,作圖痕跡中,是( )
A.以點C為圓心,OD為半徑的弧
5、
B.以點C為圓心,DM為半徑的弧
C.以點E為圓心,OD為半徑的弧
D.以點E為圓心,DM為半徑的弧
答案D
6.如圖,在公園里有一塊平行四邊形的草坪,草坪里有一個圓形花壇,有關(guān)部門計劃在草坪上修一條小路,這條小路要把草坪和花壇的面積同時平分,請在圖中畫出這條小路.(小路用AB表示)
解如圖,線段AB即為所求.
7.圖①②③④都是由24個邊長為1的小正方形組成的 4×6的網(wǎng)格,請你分別在圖②③④的網(wǎng)格中只用直尺各畫一個三角形.
要求:
(1)都與圖①中的三角形相似,但四個三角形任何兩個都不全等.
(2)三角形的頂點都是網(wǎng)格中小正方形的頂點.
解如圖.
8.☉O為△ABC的外接圓,請僅用無刻度的直尺,根據(jù)下列條件分別在圖①,圖②中畫出一條弦,使這條弦將△ABC分成面積相等的兩部分(保留作圖痕跡,不寫作法).
(1)如圖①,AC=BC;
(2)如圖②,直線l與☉O相切于點P,且l∥BC.
解(1)如圖①,直徑CD為所求;
(2)如圖②,弦AD為所求.
（人教通用）2022年中考數(shù)學(xué)總復(fù)習(xí) 第六章 圓 第23課時 尺規(guī)作圖知能優(yōu)化訓(xùn)練
