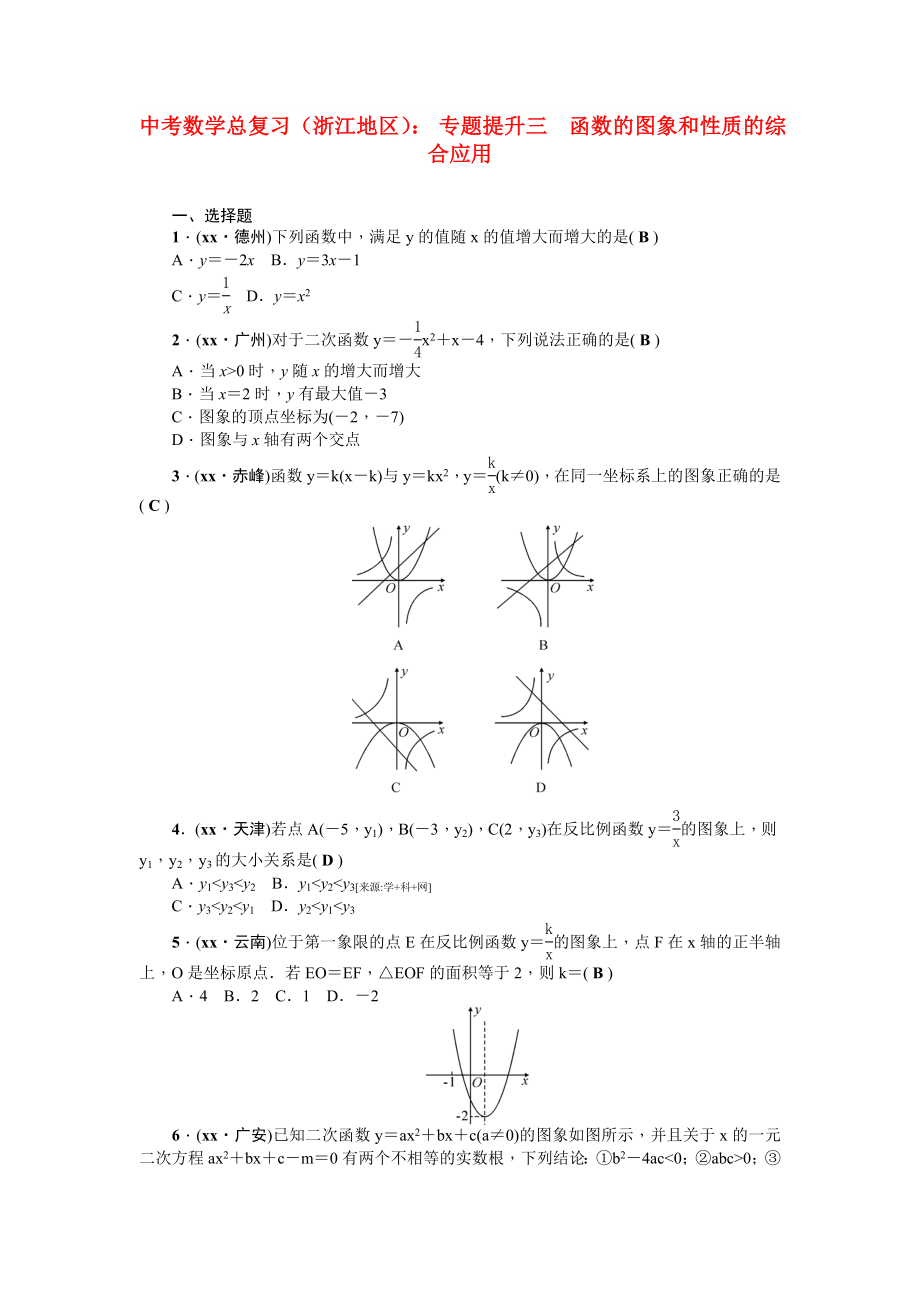
3��、實數(shù)根��,下列結(jié)論:①b2-4ac<0;②abc>0��;③a-b+c<0��;④m>-2.其中��,正確的個數(shù)有( B )
A.1 B.2 C.3 D.4
二��、填空題
7.(xx·廣安)若反比例函數(shù)y=(k≠0)的圖象經(jīng)過點(1��,-3),則一次函數(shù)y=kx-k(k≠0)的圖象經(jīng)過__一��、二、四__象限.
8.(xx·泰安)將拋物線y=2(x-1)2+2向左平移3個單位��,再向下平移4個單位��,那么得到的拋物線的表達式為__y=2(x+2)2-2__.[來源:]
9.(xx·齊齊哈爾)如圖,已知點P(6��,3)��,過點P作PM⊥x軸于點M,PN⊥y軸于點N��,反比例函數(shù)y=的圖象交PM于點A��,交PN于
4、點B.若四邊形OAPB的面積為12��,則k=__6__.
,第9題圖) ,第10題圖)
10.(xx·德州)如圖,在平面直角坐標(biāo)系中��,函數(shù)y=2x和y=-x的圖象分別為直線l1��,l2,過點(1��,0)作x軸的垂線交l1于點A1��,過點A1作y軸的垂線交l2于點A2��,過點A2作x軸的垂線交l1于點A3,過點A3作y軸的垂線交l2于點A4��,…依次進行下去��,則點Axx的坐標(biāo)為__(21008��,21009)__.[來源:學(xué)+科+網(wǎng)Z+X+X+K]
三��、解答題
11.(xx·陜西)昨天早晨7點��,小明乘車從家出發(fā),去西安參加中學(xué)生科技創(chuàng)新大賽��,賽后,他當(dāng)天按原路返回��,如圖是小明昨天出行的過程中,他距
5、西安的距離y(千米)與他離家的時間x(時)之間的函數(shù)圖象.根據(jù)下面圖象��,回答下列問題:
(1)求線段AB所表示的函數(shù)關(guān)系式��;
(2)已知昨天下午3點時��,小明距西安112千米,求他何時到家��?
解:(1)設(shè)線段AB所表示的函數(shù)關(guān)系式為:y=kx+b��,依題意有解得∴y=-96x+192(0≤x≤2) (2)12+3-(7+6.6)=15-13.6=1.4(小時),112÷1.4=80(千米/時)��,(192-112)÷80=80÷80=1(小時)��,3+1=4(時).答:他下午4時到家.
12.(xx·自貢)如圖��,已知A(-4��,n),B(2,-4)是一次函數(shù)y=kx+b和反比例函數(shù)y
6、=的圖象的兩個交點.
(1)求一次函數(shù)和反比例函數(shù)的解析式��;
(2)觀察圖象��,直接寫出方程kx+b-=0的解;
(3)求△AOB的面積��;
(4)觀察圖象��,直接寫出不等式kx+b-<0的解集.
[來源:學(xué)|科|網(wǎng)]
解:(1)y=-x-2,y=- (2)x1=-4,x2=2
(3)設(shè)y=kx+b與y軸交點為C��,∴當(dāng)x=0時��,y=-2��,∴C(0,-2),∴OC=2��,∴S△AOB=S△ACO+S△BCO=×2×4+×2×2=6 (4)-42
13.(xx·樂山)如圖��,反比例函數(shù)y=與一次函數(shù)y=ax+b的圖象交于點A(2��,2),B(��,n).
(1)求這兩個
7��、函數(shù)解析式��;
(2)將一次函數(shù)y=ax+b的圖象沿y軸向下平移m個單位��,使平移后的圖象與反比例函數(shù)y=的圖象有且只有一個交點��,求m的值.
解:(1)y=-4x+10��,y= (2)將直線y=-4x+10向下平移m個單位得直線的解析式為y=-4x+10-m��,∵直線y=-4x+10-m與雙曲線y=有且只有一個交點��,令-4x+10-m=��,得4x2+(m-10)x+4=0��,∴(m-10)2-64=0,解得m=2或m=18
14.(xx·鹽城)我市某蔬菜生產(chǎn)基地用裝有恒溫系統(tǒng)的大棚栽培一種適宜生長溫度為15~20℃的新品種��,如圖是某天恒溫系統(tǒng)從開啟到關(guān)閉及關(guān)閉后��,大棚里溫度y(℃)隨
8、時間x(時)變化的函數(shù)圖象��,其中AB段是恒溫階段��,BC段是雙曲線y=的一部分,請根據(jù)圖中信息解答下列問題:
(1)求k的值��;[來源:]
(2)恒溫系統(tǒng)在一天內(nèi)保持大棚里溫度在15℃及15℃以上的時間有多少小時��?
解:(1)把B(12��,20)代入y=中得k=12×20=240
(2)設(shè)AD的解析式為y=mx+n��,把(0��,10)��,(2��,20)代入y=mx+n中得 解得 ∴AD的解析式為y=5x+10,當(dāng)y=15時��,15=5x+10��,x=1;15=��,x==16,∴16-1=15.答:恒溫系統(tǒng)在一天內(nèi)保持大棚里溫度在15℃及15℃以上的時間有15小時.
15.(xx·安徽)如
9、圖��,二次函數(shù)y=ax2+bx的圖象經(jīng)過點A(2,4)與B(6��,0).
(1)求a��,b的值��;
(2)點C是該二次函數(shù)圖象上A��,B兩點之間的一動點,橫坐標(biāo)為x(2<x<6),寫出四邊形OACB的面積S關(guān)于點C的橫坐標(biāo)x的函數(shù)表達式,并求S的最大值.
解:(1)將A(2,4)與B(6,0)代入y=ax2+bx��,得解得:
(2)如圖��,過A作x軸的垂直,垂足為D(2��,0)��,連結(jié)CD��,過C作CE⊥AD,CF⊥x軸��,垂足分別為E��,F(xiàn),S△OAD=OD·AD=×2×4=4��;S△ACD=AD·CE=×4×(x-2)=2x-4��;S△BCD=BD·CF=×4×(-x2+3x)=-x2+6x,則S=S△
10��、OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x��,∴S關(guān)于x的函數(shù)表達式為S=-x2+8x(2<x<6),∵S=-x2+8x=-(x-4)2+16,∴當(dāng)x=4時��,四邊形OACB的面積S有最大值��,最大值為16.
16.(xx·十堰)一茶葉專賣店經(jīng)銷某種品牌的茶葉��,該茶葉的成本價是80元/kg��,銷售單價不低于120元/kg��,且不高于180元/kg,經(jīng)銷一段時間后得到如下數(shù)據(jù):
銷售單價x(元/kg)
120
130
…[來源:][來源:]
180
每天銷量y(kg)[來源:學(xué)#科#網(wǎng)]
100
95
…
70
設(shè)y與x的關(guān)系是我們所
11、學(xué)過的某一種函數(shù)關(guān)系.
(1)直接寫出y與x的函數(shù)關(guān)系式,并指出自變量x的取值范圍��;
(2)當(dāng)銷售單價為多少時��,銷售利潤最大��?最大利潤是多少��?
解:(1)∵由表格可知:銷售單價每漲10元��,就少銷售5 kg,∴y與x是一次函數(shù)關(guān)系,∴y與x的函數(shù)關(guān)系式為:y=100-0.5(x-120)=-0.5x+160��,∵銷售單價不低于120元/kg��,且不高于180元/kg,∴自變量x的取值范圍為:120≤x≤180
(2)設(shè)銷售利潤為w元��,則w=(x-80)(-0.5x+160)=-x2+200x-12 800=-(x-200)2+7 200��,∵a=-<0,∴當(dāng)x<200時��,y隨x的增大而增大��,∴
12��、當(dāng)x=180時��,銷售利潤最大��,最大利潤是:w=-(180-200)2+7 200=7 000(元)��,答:當(dāng)銷售單價為180元時��,銷售利潤最大��,最大利潤是7 000元
17.(xx·泉州)某進口專營店銷售一種“特產(chǎn)”��,其成本價是20元/千克��,根據(jù)以往的銷售情況描出銷量y(千克/天)與售價x(元/千克)的關(guān)系��,如圖所示.[來源:]
(1)試求出y與x之間的一個函數(shù)關(guān)系式��;
(2)利用(1)的結(jié)論:
①求每千克售價為多少元時��,每天可以獲得最大的銷售利潤��;
②進口產(chǎn)品檢驗��、運輸?shù)冗^程需耗時5天��,該“特產(chǎn)”最長的保存期為一個月(30天)��,若售價不低于30元/千克��,則一次進貨最多
13��、只能多少千克��?
解:(1)設(shè)y與x之間的一個函數(shù)關(guān)系式為y=kx+b��,則解得故函數(shù)關(guān)系式為y=-2x+112 (2)依題意有w=(x-20)(-2x+112)=-2(x-38)2+324��,故每千克售價為38元時��,每天可以獲得最大的銷售利潤
(3)由題意可得��,售價越低,銷量越大��,即能最多的進貨��,設(shè)一次進貨最多m千克��,則≤30-5��,解得m≤1300��,故一次進貨最多只能是1300千克.
18.(xx·舟山)小明的爸爸和媽媽分別駕車從家同時出發(fā)去上班��,爸爸行駛到甲處時��,看到前面路口時紅燈��,他立即剎車減速并在乙處停車等待��,爸爸駕車從家到乙處的過程中��,速度v(m/s)與時間t(s)的
14��、關(guān)系如圖①中的實線所示��,行駛路程s(m)與時間t(s)的關(guān)系如圖②所示��,在加速過程中��,s與t滿足表達式s=at2
(1)根據(jù)圖中的信息��,寫出小明家到乙處的路程��,并求a的值��;
(2)求圖2中A點的縱坐標(biāo)h��,并說明它的實際意義��;
(3)爸爸在乙處等待了7秒后綠燈亮起繼續(xù)前行��,為了節(jié)約能源��,減少剎車��,媽媽駕車從家出發(fā)的行駛過程中��,速度v(m/s)與時間t(s)的關(guān)系如圖1中的折線O-B-C所示��,行駛路程s(m)與時間t(s)的關(guān)系也滿足s=at2��,當(dāng)她行駛到甲處時��,前方的綠燈剛好亮起,求此時媽媽駕車的行駛速度.
解:(1)由圖象得:小明家到乙處的路程為180 m��,∵點(8��,48)在拋物線s=at2上��,∴48=a×82��,解得:a= (2)由圖及已知得:h=48+12×(17-8)=156��,故A點的縱坐標(biāo)為:156��,表示小明家到甲處的路程為156 m (3)設(shè)OB所在直線的表達式為:v=kt��,∵(8��,12)在直線v=kt上��,則12=8k��,解得:k=��,∴OB所在直線的表達式為:v=t��,設(shè)媽媽加速所用時間為:x秒��,由題意可得:x2+x(21+7-x)=156,整理得:x2-56x+208=0��,解得:x1=4��,x2=52(不符合題意��,舍去)��,∴x=4��,∴v=×4=6(m/s)��,答:此時媽媽駕車的行駛速度為6 m/s.
 中考數(shù)學(xué)總復(fù)習(xí)(浙江地區(qū)): 專題提升三 函數(shù)的圖象和性質(zhì)的綜合應(yīng)用
中考數(shù)學(xué)總復(fù)習(xí)(浙江地區(qū)): 專題提升三 函數(shù)的圖象和性質(zhì)的綜合應(yīng)用